Приближение вращающейся волны. Реакция двухуровневой среды на поле монохроматической волны

Приближение вращающейся волны.

         Рассмотрим уравнения для матрицы плотности в системе отсчета атома.

                       ρ γρ γρɺ                  + =       0 −i pE t( )(ρ ρ12 − 21)

                 11       1 11        1 11            ℏ





  ρ γρ γρɺ22 + 2 22 = 2 220 +i pE t( )(ρ ρ12 − 21)                                                                                                    (3.1)

                                                         ℏ

ρ ωρ ρɺ21 + i 21 21 + Γ 21 = i pE tℏ( )(ρ ρ11 − 22) 

Введем некоторые упрощающие предположения. Упрощения будут вполне справедливы, если вероятности обнаружить атом на уровнях 1 и 2 ^ρ₁₁ и ρ₂₂ не успевают заметно измениться за период световой волны.

         Сначала рассмотрим предельный случай: ^{ρ ρ}₁₁ ⁻ ₂₂ = const .

          Рассмотрим 3-е уравнение системы 

ρ ωρ ρɺ₂₁ + i _{21 21} ^{+ Γ} ₂₁ = i pE t( )(^{ρ ρ}₁₁ ⁻ ₂₂) и подставим в него выражение

ℏ

для                                напряженности       электрического    поля E t( )           в        явном          виде: iϕ ϕ+ ^e−i

E t( ) = ^E₀ cos( )ϕ = ^E₀ ^e        ,          где ϕ     —           фаза                                               световой волны

2

ϕ ω= ⋅ −t (k r, ) −^ϕ₀.

          Тогда

                                                                              E0 ⋅ eiϕ ϕ+ e−i  ⋅(ρ ρ−     )

 ρ ωρ ρɺ21 + i 21 21 + Γ 21 = i ^p                           11       22                 (3.2)

                                                                              ℏ          2

В правой части этого равенства есть слагаемые с "+ " и "− " оптической частотой: _e^iϕ и _e^−iϕ. Тогда решение для ^ρ₂₁ нужно искать в виде суммы двух аналогичных слагаемых:

^{ρ ρ}₂₁ ⁼ ₂₁+e^iϕ+^ρ₂₁−e^−iϕ, где ^ρ₂₁+ и ^ρ₂₁− — постоянные амплитуды.  Чуть позднее мы откажемся от предположения ^{ρ ρ}₁₁ ⁻ ₂₂ = const и амплитуды ^ρ₂₁+ и ^ρ₂₁− станут функциями времени. Пока же ^ρ₂₁₊ = const и ^ρ₂₁₋ = const. Тогда из условия ^{ρ ρ}₂₁ ⁼ ₂₁+e^iϕ+^ρ₂₁−e^−iϕ получаем в результате дифференцирования по времени:  ρ ωρɺ21 = i ' 21+eiϕ−iωρ' 21−e−iϕ.

Подставим это выражение для ρɺ21 и ρ ρ21 = 21+eiϕ+ρ21−e−iϕ в уравнение (3.2). Соберем отдельно слагаемые с _e^iϕ и _e^−iϕ и получим два уравнения:

ωρ ωρ' 21+ +i 21 21+ + Γρ21+ = i pE0(ρ ρ11 − 22)

             i                                                 2ℏ

                                                                                                         =>

−iωρ ωρ' 21− +i 21 21− + Γρ21− = i pE0(ρ ρ11 − 22)



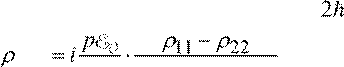 21+

                              2ℏ     Γ + i(ω ω+ ')

                     i             ρ ρ11 − 22                                  =>           ρ21− >> ρ21+

           ρ21− = 2ℏ0 ⋅ Γ + i(ω ω21 −    ')

   Тогда ^ρ₂₁+ можно отбросить в выражении ^{ρ ρ}₂₁ ⁼ ₂₁+e^iϕ+^ρ₂₁−e^−iϕ и

отбросить ^E0 e^iϕ в выражении _E0 ^{eiϕ ϕ}₊ ^e−i в правой части уравнения (3.2).

                              2                                           2

     Тогда выражение для светового поля принимает вид: E = ¹ E_0e^−iϕ — вид

2

вектора вращающегося на комплексной плоскости по часовой стрелке с угловой скоростью ω'.

По     этой   причине      рассматриваемое приближение           называется приближением вращающейся волны.

Аналогичные отбрасывания то одной, то другой части светового поля будут и в двух первых уравнениях системы (3.1).

Итак, если отбросить малое слагаемое ^ρ₂₁+e^iϕ, то недиагональный элемент матрицы плотности примет вид:

ρ ρ21 =      21−e−iϕ≡ ρɶ21e−iϕ,          где ρ^ɶ₂₁ — комплексная амплитуда недиагонального элемента ^ρ₂₁.

Откажемся теперь от первоначального предположения, что ^{ρ ρ}₁₁ ⁻ ₂₂ = const . В таком случае все равно можно считать, что

 ρ ρ21 = ɶ21e−iϕ,                                                                                  (3.3)

но только ρ^ɶ₂₁ окажется теперь функцией времени, хотя и медленной по сравнению с оптическими колебаниями.

Продифференцируем уравнение (3.3) по времени и с учетом того, что ϕ тоже зависит от времени ϕ ω= 't ⁻(k r', ') −^ϕ₀, получим:

 ρ ρɺ21 = ɺɶ21e−iϕ−iωρ' ɶ21e−iϕ                                                         (3.4)

Подставим (3.3) и (3.4) в уравнение (3.2), в духе приближения вращающейся волны, отбросим в правой части слагаемое, пропорциональное

_e^iϕ, и, после сокращения на _e^−iϕ, получим:

 ρ ρ ρɺɶ21 − Ωi ɶ21 + Γ ɶ21 = i R(ρ ρ11 −     22 )                                                                                             (3.5)

2

          Здесь введены обозначения:

Ω ≡ω ω ω'⁻ ₂₁ = − kV_z −^ω₂₁ — расстройка частоты света ω' относительно частоты перехода ^ω₂₁ в системе отсчета атома,

pE⁰

          R ≡ — частота Раби.

ℏ

Найдем теперь, как изменится правая часть первых двух уравнений системы (3.1) в приближении вращающейся волны, если подставить ρ ρ21 = ɶ21e−iϕ.

          Рассмотрим

          E t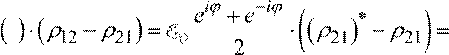    

                           eiϕ ϕ+ e−i              iϕ−ρɶ −

           = E0 ⋅(ρɶ12e    21e iϕ) ≈ E0(ρ ρɶ12 − ɶ21).

                                     2                                           2

В последнем равенстве отброшены слагаемые с удвоенной оптической частотой, так как раскачивание ^ρ₁₁ и ^ρ₂₂ на этой частоте мало эффективно.

          И действительно:

          (γρ1  11)2ω' << (ρɺ11)2ω' ≈ (ρɺ11)0 ≈ (γρ1           11)0 ,                       (3.6)  где:

           (2ω') — слагаемые на удвоенной оптической частоте,

           (0) — слагаемые на нулевой частоте.

Первое неравенство связано с тем, что ^{γ ω}₁ << 2 ', и с тем, что при дифференцировании величины, осциллирующей на частоте (2ω'), перед дифференцируемой величиной появляется сомножитель (2ω').

Приблизительное равенство в середине цепочки (3.6) связано с тем, что правая часть первого уравнения системы (3.1) имеет одинаковую амплитуду на частоте 2ω' и на частоте 0.

Правое равенство в цепочке (3.6) связано с тем, что, если нет накачки на уровень 1 и нет светового поля, то величины в двух частях равенства в точности равны по модулю. В остальных случаях это величины одного порядка.  Сравнивая начало и конец цепочки (3.6), получаем:  (ρ11)2ω' << (ρ11)0 .

То есть, осцилляциями величин ^ρ₁₁ и ^ρ₂₂ на удвоенной оптической частоте можно пренебречь.

Отбрасывая осцилляции величин ^ρ₁₁ и ^ρ₂₂ на удвоенной оптической частоте в двух первых уравнениях системы (3.1), получим ту же систему уравнений в новом виде:

ρ γρ γρɺ11 + 1 11 = 1 110 −i R₂ (ρ ρɶ12 − ɶ21) 

                                         0 + i R(ρ ρɶ12 − ɶ21)                                      (3.7)

      ρ γρ γρɺ22 + 2 22 = 2 22

                                                    2

ρ ρ ρɺɶ21 − Ωi ɶ21 + Γ ɶ21 = i R2 (ρ ρ11 − 22)

Это и есть уравнения для матрицы плотности в приближении вращающейся волны.

          Для решения любой квантовомеханической задачи нужно сначала решить систему уравнений (3.7), затем по полученной амплитуде ρ^ɶ₂₁ найти недиагональные элементы