Скоростные уравнения или уравнения баланса. Физический смысл скоростных уравнений

Скоростные уравнения или уравнения баланса.

Скоростные уравнения — это приближение, которое получается из условия

 ρ^ɺɶ21 = 0

и уравнений для матрицы плотности в приближении вращающейся волны:

ρ γρ γρɺ11 + 1 11 = 1 110 −i R₂ (ρ ρɶ12 − ɶ21) 

                ρ γρ γρ22

                ɺ   + 2 22 = 2 220 +i R(ρ ρɶ12 − ɶ21),                                   (5.1)

                                                     2

ρɺɶ     − Ωi ρ ρɶ21 + Γ ɶ21 = i R₂ (ρ ρ11 − 22) 21

          где

R ^{= pE0} — частота Раби, ℏ

p p e dV — недиагональный матричный элемент проекции V=∞ дипольного момента перехода на единичный вектор поляризации световой волны,

    Ω =ω− kV_z −^ω₂₁ — расстройка частоты света относительно частоты перехода в системе отсчета молекулы,

^{ρ ρ}₂₁ = ^ɶ_21e^−iϕ — недиагональный элемент матрицы плотности,  ϕ ϕ ω⁼       ₀ +     t − kz — фаза световой волны.

Нас в дальнейшем будет интересовать взаимодействие двух световых волн со средой. Если световые волны встречные, то в системе отсчета молекулы две волны будут иметь разные частоты, даже если в лабораторной системе отсчета частоты одинаковы. В таком случае в системе отсчета молекулы амплитуда суммарного светового поля испытывает биения, поэтому условие ρ^ɺɶ₂₁ = 0 не выполнено даже для стационарных явлений с двумя световыми волнами.

Однако при условии слабого светового поля, когда G <<1, так называемые когерентные нестационарные эффекты в наблюдаемых величинах усредняются, и скоростные уравнения дают хорошее приближение.

         Подставим ρ^ɺɶ₂₁ = 0 в третье уравнение системы (5.1) и получим

          

                              =>

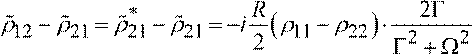          i R2 ɶ − ɶ21) = R2(ρ ρ11Γ− 22) ⋅L ΩΓ , где

(ρ ρ12

2

                ^L( )x ^{≡ 1} ₂ — лоренцевский контур           =>

1+ _x

ρ γρ γρɺ11 + 1 11 = 1 110 − R2Γ2             Ω 

                                                   (ρ ρ11 − 22)⋅L Γ 

                                                                                  

ρ γρ γρɺ22 + 2 22 = 2 220 + RΓ2(ρ ρ11 − 22)⋅L ΩΓ 

                                                    2

Умножим систему на распределение концентрации по лучевой скорости ^N_0Vz и получим

                ɺ                       N0        R2(        )  Ω 

                              +γ1 1N       =γ −            N      −

             _N1_Vz               Vz           1 1Vz         2Γ     1Vz     N2Vz ⋅L Γ 

                                                                                                            (5.2)

Nɺ2V + 2 2N V = 2N20 + R2Γ2(N1Vz − N2Vz )⋅L ΩΓ 

                     z                      z                      z

Это почти скоростные уравнения, осталось заменить величину R² на более традиционное выражение.

---------

Для получения нового вида уравнений нам понадобятся две новые величины: J и σ.

Введем в рассмотрение J — плотность потока фотонов. Эта величина связана с интенсивностью света I , которая представляет собой плотность потока энергии светового поля. Тогда

           J ≡ ^I

             где 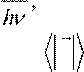I ≡ S , где угловые скобки означают усреднение по времени,

S ^{= c }E H, ^ — вектор Пойнтинга.

₄π

               Рассмотрим цилиндр со световым полем, объемная плотность которого

w, а фазовая скорость —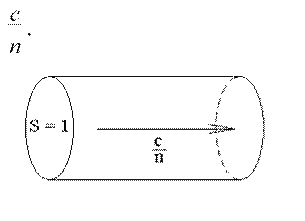

c

                                                                        Пусть площадь сечения цилиндра равна единице, а длина —    . Тогда n c

объем цилиндра равен их произведению  , а энергия светового поля в этом

n

c

объеме равна w  . Вся эта энергия в единицу времени пройдет через n

единичную площадку. Следовательно,

            I = w ^c .

n

          Объемную плотность энергии w можно выразить через амплитуду светового поля E₀. И действительно            w =odD E, i d+ B H, it.

              В оптике µ= 1 и µ εH =   E в бегущей световой волне, тогда

2 2

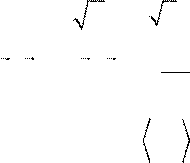       w = 1 {(D E, ) (+ B H, )} = 1 {ε µE2 + H2} = 1 εE2 = n E .

                          8π                           8π                      4π            4π

E2

           E = E0 cos(ωt)      =>           E2 =            =>

= ⁿ2 2E0 .            w

8π   Тогда

= w⋅ c ⋅ 1 = ncE₀2 .

           J

n hν πω8 ℏ

---------

          Оказывается, что в этом выражении нужно заменить n → n₀ .

          Такая странность имеет две причины.

Во-первых, часть энергии светового поля принято считать энергией, запасенной в среде. Дело в том, что D = E + 4πP, где поляризация P имеет два слагаемых: резонансное ^P_рез и нерезонансное ^P_нерез . Резонансный вклад связан с тем, что молекула может поглощать или излучать свет, только одновременно находясь на двух уровнях энергии. Следовательно, резонансный вклад в поляризацию неразрывно связан с частичным заселением возбужденного уровня энергии. По этой причине соответствующую энергию рассматривают, как энергию среды, а не как энергию светового поля. Тогда обозначим вектор электрического смещения без резонансного вклада в поляризацию, как  D₀ = E + 4πP_нерез = n E₀² , что аналогично D E= + 4π εP = E n E= ² .

        Соответственно объемная плотность энергии w₀ ^{= n02 2}8^Eπ⁰ .

Кроме того, рассматривая обратное воздействие среды на волну, мы договорились рассматривать свет, как будто он распространяется со скоростью c          c

 , а не       . n₀         n

          В результате

J = w⋅ ⋅ = . n₀ hν πω8 ℏ

---------

          Введем теперь в рассмотрение новую величину σ — сечение поглощения, которая по своему физическому смыслу должна быть равна площади тени молекулы. Через сечение поглощения σ может быть выражен коэффициент поглощения ℵ.

Коэффициент поглощения определяется зависимостью изменения интенсивности света по мере его распространения в поглощающей среде:

I z( ) = I(0)⋅e^−ℵz  С учетом равенства J ≡ ^I получим hν  J z( ) = J(0)⋅e^−ℵz.

---------

(N₁ − N₂) — эффективная концентрация поглощающих свет молекул, так как при одинаковых заселенностях верхнего и нижнего уровней энергии число переходов снизу вверх равно числу вынужденных переходов сверху вниз, и поглощение света отсутствует.

(N₁ − N₂)⋅S dz⋅ — число этих как бы поглощающих свет молекул в объеме