Введение в механику сплошных сред. Движение жидкостей и газов. Способы описания движения жидкости. Основные уравнение гидродинамики

Пусть у нас имеется плоская волна, распространяющаяся в направлении x, тогда, как и в случае с волнами в упругой среде:

                                                                         ∂²P    1 ∂²P

                                                                                  2 − 2           2 = 0,

                                                                         ∂x     c   ∂t

и функция

P(x,t)= f (x −ct)+ g(x +ct)

будет решением этого уравнения. Переменная c, очевидно, является скоростю звука в среде. Для гармоничных волн:

P = Acos(kx − ωt),

2π  2π      λ        ω где k =        , ω=       и c =    =       . λ      T        T         k

2.3.3. Скорость звука в газах

∂P

Отчего зависит скорость звука c =. Можно легко получить эту ∂ρ

зависимость для газа. Для адиабатических процессов P = ρ^γconst , где c^P >1,  c_P и c_V - теплоемкости газа при постоянном давлении и

γ =

c_V

постоянном объеме. Таким образом,

∂P                   γ−1         P

=const +γρ =γ

∂t                            ρ

и мы в результате получаем:

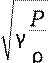c =  ≈c = 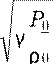 .  Отметим, что скорость звука c растет с ростом ρ₀, но с ростом ρ₀растет и P₀ , значит, c растет с ростом давления газа P₀ . 

Оценки: 

•  для атмосферного воздуха: γ≈1,4; ρ =1,3 кг₃ ; P ≈10⁵Па ; c ≈ 330 ^м . м  с

∂P

•  для жидкостей       существенно больше. Поэтому для воды ∂ρ

м

                c ≈1200 . 

с

2.3.4. Гармоническая волна

Рассмотрим, как изменяются скорости частиц при такого рода волнах. Воспользуемся уравнением:

∂v 1 ∂P + = 0.

                                                                            ∂t    ρ₀ ∂x

Для гармоничной волны: 

∂P

 = −Aksin(kx − ωt);

∂x

                                                                    ∂v    Ak

                                                                            =       sin(kx − ωt).

                                                                    ∂t     ρ₀

Поскольку среднее значение скорости равно нулю, получаем:

Ak

v = −      cos(kx − ωt), ωρ₀

или 

A

v = −      cos(kx − ωt), cρ₀

т.е. скорости частиц так же совершают колебательное движение, причем в противофазе с колебательным изменением давления.

2.4. Прохождение звука через границу раздела двух сред

2.4.1. Коэффициенты отражения и прохождения

Рассмотрим прохождение звука через границу раздела двух сред. Пусть две среды, отличающиеся плотностью (ρ₁ и  ρ₂) и скоростями звука (с₁ и с₂) имеют плоскую границу раздела, перпендикулярную к x при x = x₀. Пусть волна распространяется вдоль xв среде (1). На границе раздела раздела должно выполняться условие непрерывности. Без ограничения общности будем считать x₀ = 0. В среде (1) будут распространяться две волны: падающая на границу раздела 

P₁⁺ = Acos(k₁x − ω₁t);

v₁⁺ = − ^A cos(k₁x − ω₁t)

ρ1c1

и отраженная: 

P₁⁻ =VAcos(−k₁x − ω₁t);

v₁⁻ = − ^A V cos(−k₁x − ω₁t),

ρ1c1

где V - коэффициент отражения. В среде (2) распространяется одна волна, прошедшая через границу раздела:

P₂ =WAcos(k₂x − ω₂t);

A v₂ = −W cos(k₂x − ω₂t),

ρ2c2

где W - коэффициент прохождения. Условия непрерывности на границе при x = x₀ = 0:

P1+ + P1− = P2 и v1+ +v1− =v2 .

Конкретно с учетом x = 0: 

(1+V)Acos(ω₁t)=WAcos(ω₂t);

(1−V^{) A} cos(ω₁t)=_W      ^A cos(ω₂t) ρ1c1       ρ2c2

Очевидно, это может выполняться только при ω₁ = ω₂ , т.е. частота звуковой волны не меняется при прохождении границы раздела.  Если так, то: 

1+V =W ;

(1−V ₎ ^A =W ^A . ρ1c1     ρ2c2

Решим это уравнение:

ρ c

                                                                       1+V =   ^{2   2} (1−V );

ρ1c1

 ρ c −ρ c

V  = 2 2 1 1 ; ρ2c2 + ρ1c1

                                                                                             2ρ²c²       .

W  =

ρ2c2 + ρ1c1

Величину Z =ρc называют волновым сопротивлением или импедансом. 

2.4.2. Граница вода-воздух 

Рассмотри две ситуации, прохождение волны из более плотной среды в менее плотную и наоборот. 

₁₀3 кг

                               Z^воды ≈ ρводы cвозд ≈        м 3 1200 ≈ 3⋅103 .

Например,

Zвозд                                        ρвозд cводы    1,3 кг3 330 м

ρ¹c¹<<1; V ≈1; W ≈ 2.

1) воздух-вода:

ρ2c2

P₁⁺ + P₁⁻ = A[cos(k₁x − ωt)+ cos(−k₁x − ωt)]= 2Acos(k₁x)cos(ω₁t)

-  стоячая волна с максимумом амплитуды при x = 0. 

P₂ = 2Acos(k₂x − ωt)

-  волна удвоенной амплитуды.

ρ¹c¹ >>1; V ≈ −1;  W ≈ 0.

2) воздух-вода:

ρ2c2

P₁⁺ + P₁⁻ = A[cos(k₁x − ωt)− cos(−k₁x − ωt)]= 2Asin(k₁x)sin(ω₁t)

- стоячая волна с нулевой амплитудой вблизи границы раздела. Коэффициент прохождения через границу раздела - ноль.

Следствия: 

•  рыбы слышат нас, а мы их нет;

•  тонкое стекло сильно заглушает звуки с улицы.

В уравнениях идеальной жидкости мы не рассматривали силы вязкого трения. На самом деле они всегда присутствуют. Рассмотрим их влияние на течение жидкости, и условия, при которых их роль становится пренебрежимо мала.

3. ВЯЗКАЯ ЖИДКОСТЬ

3.1. Силы вязкого трения

Рассмотрим жидкость между двумя плоскими параллельными пластинами, площадью S . Верхняя пластина движется относительно нижней со скоростью v. Если зазор h между пластинами мал:  h << S , то опыт показывает: 

v

F = ηS h

Верхний слой жидкости движется вместе с пластиной со скоростью v, нижний покоится (v=0). В слое толщиной h при этом возникает сдвиговая сила трения F, пропорциональная S :

                                                                            F      v      dv

                                                                                 = η   ≈ η      .

                                                                            S      h      dh

Величина η - динамическая вязкость жидкости. Во многих задачах коэффициент вязкости входит в виде отношения . Величина ν =  

называется кинематической вязкостью. Коэффициент вязкости зависит от температуры, причем при повышении температуры вязкость жидкости падает, а вязкость газов, как правило, слегка возрастает.

3.2. Уравнение Навье–Стокса

Для потока идеальной жидкости мы получили уравнение Эйлера: 

dv

ρ = −grad(P). dt

Если учесть силы вязкого трения, то вид этого уравнения изменится. 

Снизу того же слоя:                                                     ∆F₁ = F₁′−F₁′′= ηdx₁dx_{3       2}¹dx₂ dx₂

Сила, приложенная к единичному объему составляет:

                                             f₁ = ∆F1 =        1         ηdx1dx2dx3d2v21 ;

                                                        ∆V    dx₁dx₂dx₃                                 dx₂

f₁ = ηd2v1 .

2

dx₂

Если мы учтем изменение скорости v₁ вдоль направления x₃, то получим:

f1 = η⎡⎢d2v21 + d2v21⎤⎥ .

                                                                                     ⎣dx₂          dx₃ ⎦

Что будет, если скорость меняется и вдоль x₁? Можно показать, что в этом случае для несжимаемой жидкости справедливо:

f₁ = η⎡⎢d2v1 + d2v21 + d2v21⎤⎥ .

2

                                                                            ⎣dx1         dx2         dx3 ⎦

Заметим, что  

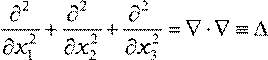, где ∆ – оператор Лапласа. Окончательно, сила вязкого трения, отнесенная к единице объема: 

 f_i = η∆v_i или 

 f =η∆v .

При учете этих сил, в уравнении Эйлера нужно добавить еще один член: 

dv

ρ = −grad(P) + f ; dt

dv

ρ = −grad(P) + η∆v. dt

Найденное уравнение называется уравнением Навье–Стокса для жидкости