Однородная и неоднородная (доплеровская) ширина спектральной линии. Дисперсионные соотношения Крамерса-Кронига

Дело в том, что в остальных точках δ-функция равна нулю, и величина второго сомножителя несущественна, поэтому можно положить, что второй сомножитель — постоянная величина равная значению второго сомножителя при таком V_z, при котором аргумент δ-функции равен нулю. Под интегралом при этом останется δ-функция, интеграл от которой по определению равен единице.  Приравниваем аргумент δ-функции нулю:

ω− kV −ω                      z         0 = 0 => γ	ωω− Vz =          0 k	=>	− z  e  U 	−      0  = e  kU 	=>
−ωω− 0 2              Iω~ e  kU 	=>

                                                                                                                                           V ²           ωω−                                                                                               ²

−ωω− 0 2

I_ω= I₀ ⋅e ^{ kU } — это и есть доплеровский контур спектральной линии.

1

Ширина этого контура в шкале частот на уровне          равна ∆ω= 2kU . e

---------

В заключении повторим, что спектральный контур линии поглощения или излучения каждой одиночной молекулы или атома — это контур лоренцевской формы:

           Iω= I0 ⋅ 1  2 .

ωω−      0  1+ γ 

Ширина этого контура на половине его высоты равна 2γ — это однородная ширина спектральной линии.

Если однородная ширина линии мала по сравнению с доплеровским сдвигом частоты связанным с тепловым движением молекул, то спектральная линия имеет доплеровский контур:

−ωω− 0 2

              Iω= I0 ⋅e  kU  .

1

              Ширина доплеровского контура на уровне  равна 2kU — это

e

неоднородная ширина спектральной линии.

В случае, когда однородная и неоднородная ширины спектральной линии — это величины одного порядка, контур спектральной линии имеет фойхтовскую форму:

+∞−Vz 2          Iω~ ∫  ⋅_e ^{ U } ⋅dV_z .

−∞1+ω− kVγz −ω0 

Факультатив. Дисперсионные соотношения Крамерса-Кронига.  Пусть единственное окно в комнате закрыто узкополосным светофильтром, который пропускает свет только с частотой ω. Строго монохроматический свет обязан быть по времени от минус до плюс бесконечности. Это с одной стороны.

С другой стороны, если свет за окном в какой-то момент включить, то в комнате свет не может появиться раньше этого момента независимо от того, насколько узкополосный светофильтр закрывает окно.

Это условие накладывает связь на функции ℵ(ω) и n'(ω), которая должна выполняться независимо от природы светофильтра.

                        Пусть τω( ) — амплитудный коэффициент пропускания светофильтра.

Тогда комплексные амплитуды света на входе и на выходе светофильтра связаны соотношением:

         E₀вых (ω τω) = ( )⋅ E₀вх (ω)

Рассмотрим бесконечно короткую вспышку света перед светофильтром в виде δ-функции Дирака:  Eвх(t) =δ(t).

                      Ее Фурье-образ — комплексная амплитуда света на входе светофильтра:

                                                                                            E₀вх ( )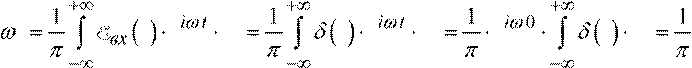                                             t  e   dt        t          e                dt    e        t          dt

          Комплексная амплитуда на выходе светофильтра:

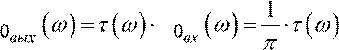           E E        .

Тогда напряженность светового поля на выходе светофильтра, как функция времени имеет следующий вид:

1  +∞          −i tω ω= Re+∫∞E0вых ( )ω ⋅e−i tωdω =

          Eвых( )t =  ⋅ ∫ E0вых ( )ω ⋅e      d           

2   0            

−∞

    = Re_+0∫∞π1 ⁻i tω ω = 1 ⋅Re+∫∞τω( )⋅e−i tωdω.

                                   ⋅τω( )⋅e      d       π  0                                 



          До момента времени t = 0, в который произошла вспышка света перед фильтром, света после           светофильтра        быть не           должно E_вых(t) = 0. Следовательно, при t < 0:

                     +∞                       

       Re ∫ τω( )⋅_e^{−i tω}dω_ = 0.

_

                       0                              

Если светофильтр представляет собой однородную среду толщиной z₀ , то амплитудный коэффициент пропускания такой среды имеет вид:

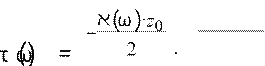n '(ωω)⋅

i z₀  e e ^c .

          Тогда получим

  Re+∫∞e−ℵ ⋅(ω) z0 ⋅ in '(ωω)⋅ z0 −i tω ω = 0 при t < 0.

                                              2         e      c           ⋅e       d

                      ₀                                                            

Этим интегральным соотношением связаны коэффициент поглощения любой среды ℵ(ω) и ее вещественный показатель преломления n'(ω).

В свою очередь с величинами n'(ω) и ℵ(ω) связаны вещественная αω'( ) и мнимая αω''( ) части комплексной поляризуемости атома. Эта связь оказывается проще для малой концентрации атомов. В этом случае

ℵ( )ω = 2ω_c n''( )ω



n = +1 2παN и n( )ω ω= n_'( ) + i n⋅ _''( )ω .

                                              ^αω αω αω( ) = _'( ) +_i⋅      _''( )



Крамерсу и Кронигу удалось выразить из интегрального соотношения одну функцию αω_'( ) через другую αω_''( ) и наоборот:

_αω'( ) =π2 ⋅P+∫∞αω ωω ω''(2 ₋0)⋅2 0 ⋅dω0

0  0

         ^                        _+∞αω_'( ₀)  — соотношения Крамерса-Кронига.

₂ω

                              

                                      ₀     0

Здесь ^P∫ — интеграл в смысле главного значения, α α α= '+i⋅ '' — комплексная поляризуемость атомов.

Факультатив. Лоренцевская форма спектральной линии и дисперсионный контур показателя преломления не зависят от модели атома Томсона.  Мы получили лоренцевский контур линии поглощения через рассмотрение комплексной поляризуемости атома Томсона.

Модель атома Томсона не слишком убедительна. Не означает ли это, что на самом деле однородный контур линии поглощения без учета эффекта Доплера не является лоренцевским?

Нет. Оказывается, что лоренцевская форма линии поглощения получается при весьма общих предположениях относительно механизма излучения света атомом.  Для лоренцевской формы линии излучения Iω= I₀ ⋅ ¹ ₂ достаточно

 Ω 

1+ _γ

экспоненциальной формы зависимости от времени амплитуды излучения атомом светового цуга E E⁼ ₀ ⋅e^−γt ⋅e^−iω0t , так как:

          E ( )ω = 1 +∫∞            i tω = 1 ⋅ E⁰

                                                   E( )t ⋅e    dt

                             π                        πγ− Ωi

                                        .

Iω= 8cnπµE0( )ω2

          Контур линии поглощения повторяет контур линии излучения