Параллелепипед Френеля. Лучевая и фазовая скорости световой волны в кристалле. Лучевая и фазовая скорости в простейшем частном случае

Экзамен. Параллелепипед Френеля.

За одно полное внутреннее отражение не удается получить разность фаз  для двух линейных поляризаций. За два полных внутренних отражения можно набрать сдвиг фаз  между двумя линейными поляризациями, что позволяет получить циркулярно поляризованный свет из света линейной поляризации.

 

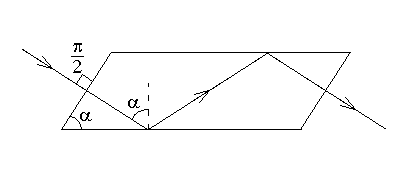
                 Свет нормально падает на переднюю грань параллелепипеда Френеля.

Угол α при вершине параллелепипеда подобран так, чтобы выполнить условие

2⋅δϕ=π,      где δϕ= arctg Im(r^|| ) − arctg ^Im(^r⊥) .    При    этом    на                                                 входе                                  в

                    2                                Re( )r||              Re(r⊥)

параллелепипед свет имеет линейную поляризацию, приведенную на нижеследующем рисунке.

 

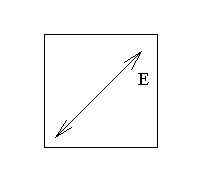
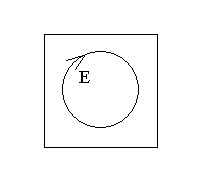
          А на выходе свет имеет круговую поляризацию.

 

Кристаллооптика.

            Экзамен. Направление векторов D E B H k S,                      , ,                                             , ,     для плоской световой

волны в кристалле.

Рассмотрим сначала решение волновых уравнений для векторов E и B в виде комплексных плоских монохроматических волн: E = E e₀ ^{i k r}( ^{, −ωt}) и

B = B e₀ ^{i k r}( ^{, −ωt}). Вещественные поля представляют собой вещественную часть этих комплексных выражений. Далее будем рассматривать вещественные плоские волны.

Для нас будет важно, что оба поля зависят от координат и времени только через их комбинацию в виде (k r, −ωt). Обозначим эту комбинацию буквой ϕ⁼ (k r, ) −ωt .  ϕ — это фаза волны без учета начальной фазы, которая может оказаться различной для различных проекций векторов E(ϕ) и B(ϕ).

        Рассмотрим производную по времени, например, от вектора E(ϕ):

           .

                     ∂t             dϕ ∂t           dϕ           ∂t                      dϕ

          Что в операторном виде можно записать, как:

                ∂⋅          d ⋅

             = −ω .

                ∂t          dϕ

            Рассмотрим производную от вектора E(ϕ) по x координате:

∂E∂( )xϕ ϕ= dEd( ) ⋅ ∂ϕ= dEdϕ( )ϕ ⋅ ∂(k r,   −ωt) = dEdϕ( )ϕ ⋅ ∂(k xx + k yy + k zz −ωt) = kx ⋅ dEϕ( )ϕ

                               ϕ ∂x                         ∂x                                      ∂x                 d

          Тогда для вещественной плоской монохроматической волны:

                ∂⋅         d ⋅

        ∂x = kx d_ϕ.

          Тогда

                                ∂         ∂         ∂             d               d              d          d

  ∇ = ex ∂_x + ey ∂_y + ez ∂_z = e kx x _dϕ+ e ky y _dϕ+ e kz z _dϕ ϕ= k _d                                                            .

(∇,D) = 0 

∇,E = −1c ⋅ ∂∂Bt

          Подставим эти соотношения в 4-е уравнения Максвелла           

(∇,B) = 0 

∇,H = 1c ⋅ ∂∂Dt

ρ= 0

для прозрачной  , но анизотропной среды, для которой диэлектрическая  j = 0

проницаемость ε — тензор второго ранга, и получим:

k ddϕ,D = 0                    ddϕ(k,D) _{= 0}

                                                                        

       k dϕ,E =ω dϕB             d k,E = ddϕωc B



                          d              c d                                  dϕ

                                                         =>                                               =>

         k d ,B = 0                         ddϕ(k,B) = 0

                   dϕ                                           



                   d           ω

k dϕ,H = − c ddϕD  ddϕk,H = − ddϕωc D

(k,D) = const 

k,E =^ω_c B+ const

                                              ,

(k,B) = const



^k,H = −^ω_c D + const

где const — константы, независящие от ϕ. То есть константа не зависит ни от времени, ни от координат, так как вся зависимость электрического и магнитного полей от времени и координат есть только через зависимость от ϕ⁼ (k r, ) −ωt .

Нас интересуют электромагнитные поля на оптических частотах, а не постоянные поля, поэтому константы в правых частях равенств можно считать равными нулю:

(k,D) = 0 

^k,E =^ω_c B

                                  .

(k,B) = 0 

k,H = −ωc D

          Факультативная вставка.

Обсудим подробнее, почему константы равны нулю.            Рассмотрим, например первое уравнение системы:

          (k,D) = const       =>       k_{x x}D + k_{y y}D + k_{z z}D = const.

Здесь k_x,k_y,k_z — константы, а D — вещественная плоская монохроматическая волна. Тогда проекции ^{D D D}_x, _y, _z пропорциональны косинусам одной частоты ω, возможно с разными начальными фазами. Равенство k_{x x}D + k_{y y}D + k_{z z}D = const можно рассматривать, как Фурье

разложение константы, стоящей в правой части равенства. Если рассмотреть Фурье разложение константы, то в нем не могут присутствовать частоты отличные от нулевой частоты, что следует из единственности Фурье разложения.           Следовательно,    константа           в        правой        части           равенства kx xD + ky yD + kz zD = const равна нулю. Тогда из равенства (k,D) = const следует равенство (k,D) = 0.

Аналогично остальные равенства системы уравнений можно расписать в декартовых координатах и пользуясь единственностью Фурье разложения получить:

(k,D) = 0 

^k,E =^ω_c B



                                  .

(k,B) = 0



^k,H_ = −^ω_c D

          Конец факультативной вставки.

    Добавим сюда уравнение S и заменим вежде вектор H на вектор B, так как B H=µ , а в оптике µ=1. В результате получим пять соотношений:



(k,D) = 0

                                                                        k ⊥ D

    (k,E) =ωc B                         B EB ⊥⊥ k

             k,B = 0                       =>                           .

                                                                         B D⊥

        _k,B_ = −^ω_{c D}                                 _S ⊥ E

                       c                                              S ⊥ B

               _S = [_EB, ]

                      4π

          Факультативно     заметим,     что     из      ортогональности           векторов     с вещественными координатами следует ортогональность тех же векторов с комплексными координатами. Это ортогональность не в том смысле, что скалярное произведение равно нулю, а в том смысле, что вещественным поворотом осей координат можно обнулить все координаты кроме одной для одного вектора и одновременно обнулить все координаты кроме другой для второго вектора.

Из полученных соотношений ортогональности видно, что вектор B перпендикулярен 4-м остальным векторам k,DE, ,S . Эти 4-е вектора лежат в одной плоскости, перпендикулярной вектору B.

          Сгруппируем соотношения ортогональности по три:

k ⊥ D



k ⊥ B B D⊥ 		=>	векторы k,DB,     взаимно ортогональны,
S ⊥ E            S ⊥ B E B⊥ 		=>	векторы S, ,EB взаимно ортогональны.

Рассмотрим рисунок, на котором вектор B перпендикулярен плоскости рисунка, тогда остальные 4-е вектора окажутся в плоскости рисунка:

 

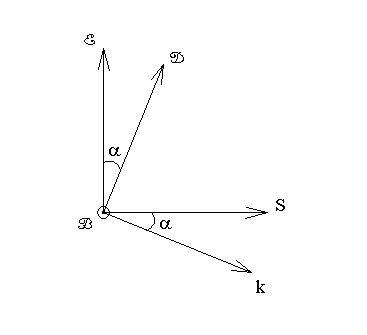
E ⊥ S  Из  следует, что угол между векторами E и D равен углу между D ⊥ k

векторами S и k . Обозначим этот угол за α:

 α^≡ (D E, ) ⁼ (S k, )                                                                           (7.1)

---------

Напомним, почему в кристалле векторы E и D различаются по направлению.

В кристалле D E=εˆ , где εˆ — тензор диэлектрической проницаемости. εˆ — симметричный тензор второго ранга. В тензорной алгебре есть теорема о том, что симметричный тензор второго ранга поворотом системы координат можно привести к диагональному виду:

                         ^ε_x       0     0 

                                            

            D ⁼  0 ^ε_y          0 ⋅E.

                         0    0 εz 

Если тензор диэлектрической проницаемости диагонален, то оси координат x y z, , — совпадают с главными диэлектрическими осями кристалла по определению главных диэлектрических осей.

Умножение вектора E слева на диагональный тензор εˆ означает разное растяжение по осям x y z, , , растяжение в ^εεε_x, _y, _z раз соответственно. Растяжение по осям различно, поэтому D вектор произведения