Интенсивность пропорциональна квадрату амплитуды. Соотношение неопределенности Гейзенберга. Разложение светового поля по плоским монохроматическим волнам

.

Равенство достигается только для светового импульса гауссовой формы:  E( )t = E_0e^−αt2 cos(ω₀t),  то есть когда огибающая импульса является гауссовой кривой E₀e t2 . −α

Чтобы убедиться в равенстве  нужно вычислить ∆ω и ∆t , которые в свою очередь выражаются через . А эти величины выражаются через спектральную плотность интенсивности Iω и через зависимость интенсивности от времени I t( ).

---------

          Найдем ∆t .

          Интенсивность пропорциональна квадрату амплитуды, тогда:

I t( ) = 4cnπµE2( )t          = 4cnπµ (E0e−αt cos(ω0t))2 = cnπµ(E0e−αt )2cos2(ω0t)=

4

            .                  =>

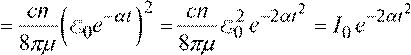           I t( )= I₀⋅e−2αt²

          Тогда

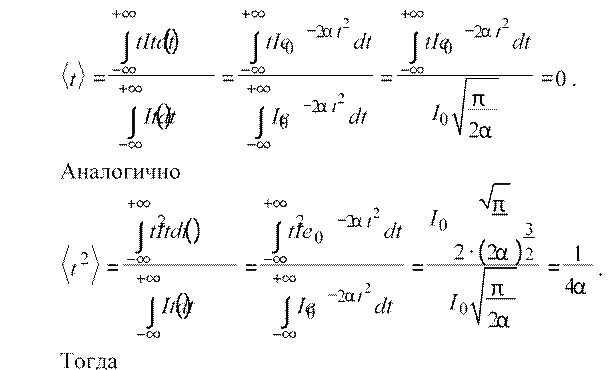
          ∆ =t .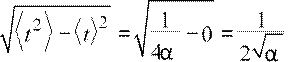

---------

          Найдем теперь ширину спектра светового импульса ∆ω.

                E( )t = E0e−αt2 cos(ω0t) = E0e−αt2 eiω ω0t + e−i 0t — световой импульс. Тогда

2

Фурье образ напряженности светового поля будет иметь вид:

           E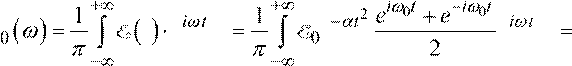 t e                                                          dt     e                            e     dt   

            



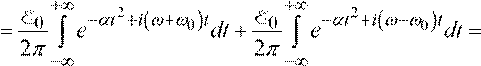
                                 (ωω+ 0)2 +     −α ωωt −αi ( + )t−(ωω+ 0)2

                  E e− ⁴α ∫∞e       2               0            4α2    dt +

−∞

E −(ωω− 0)2 +∫∞ −α ωωt  i ( − 0)t−(ωω4− 20)2 dt = 2−

α e      α          α  e    4

−∞

                                   (ωω+ )2

                        E −           0    +∞ −α ωωt− i ( + )2                        (ωω− )2

            = 0 e         4α ∫ e            2α 0  dt + E0 e− 4α0                            +∫∞e−α ωωt−2αi ( − 0)2dt =

                     2π             −∞                                          2π              −∞

                                  (ωω+ )2                               (ωω− )2

             =E −                       0 π E0 e− 4α0 π=

                         0 e            4α+

                     2π                  α π2                     α

                                       (ωω+ )²             (ωω− )² 

                           E     4 + e     4          

                        = 2 πα⁰ e.

                                                                      

Из этих двух слагаемых одно можно отбросить. Дело в том, что частоты ω и ^ω₀ положительные, и нас интересует случай, когда спектральная плотность интенсивности около нулевой частоты очень мала. Эти условия эквивалентны неравенству . В таком случае второе слагаемое может иметь порядок единицы при условии ωω^≈ ₀, а первое слагаемое всегда много меньше единицы, и его можно отбросить. Тогда

−(ωω− 0)²

E

               E₀( )ω= ⁰ e    ^4α — Фурье образ светового импульса гауссовой

2 πα

формы, как функции времени, имеет гауссову форму, как функция частоты.

Откуда можно найти спектр светового импульса:

                                                                                                (ωω− )2

^cn       ( )^{2      cn}E⁰2 ⋅e− ^2α0 , который тоже имеет гауссову  Iω= 8πµ⋅ E₀ ω = 32πµα₂

форму.

Средняя частота светового импульса, как следует из его симметрии, равна ω₀, и ее можно не вычислять. Тем не менее вычислим ее:

                          +∫∞               +∫∞               +_∫∞      ^{cn 0}2 ⋅e−(ωω−^2α0)2dω

E ω ωI dω    ω ω ωI dω    ₂

cnE

                                  0                     −∞                         32πµα²

_−∞

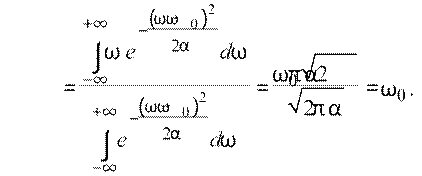
       В данном случае ширину светового импульса в шкале часто проще

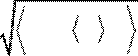вычислить      по      формуле           ∆ω ω ω⁼      ( ⁻     )² ,     а       не                         по      формуле

∆ω ω ω=  ² −        ² . Тогда

       

+∞

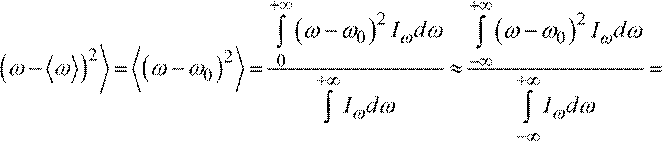
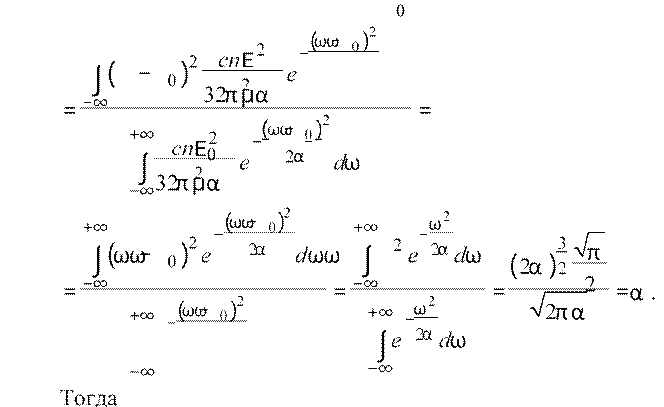                                ωω             0                 2α dω

                                 ∫ e        ^2α dω

                ∆ω ω ω=          ( −  )² = α.

---------

          И, наконец 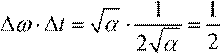  . Равенство доказано.

Факультатив. Соотношение неопределенности Гейзенберга.

Рассмотрим соотношение неопределенности частоты и времени в сочетании с выражением для энергии фотона:

             ∆ω⋅∆ ≥t  1

                          2 .

E = hν ω= ℏ  Умножим первое равенство на ℏ ^{≡ h} и с учетом второго равенства 2π

получим:

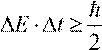               — соотношение неопределенности Гейзенберга для энергии и времени, справедливое как для фотона, так и любой другой частицы.

Это соотношение означает, что нельзя одновременно знать и время возможной регистрации фотона, и ожидаемую энергию фотона при его регистрации.

Чем точнее будет известно время регистрации фотона, тем больше неопределенность в энергии фотона. Это следует из того, что для точного определения момента необходимо, чтобы световой импульс был коротким. При этом спектр импульса автоматически, на основе свойств преобразования Фурье, оказывается широким. Энергия фотона пропорциональна частоте, поэтому и энергия фотона, который можно зарегистрировать, оказывается в состоянии с большой неопределенностью.

---------

          Заметим, что аналогичное соотношение неопределенности можно написать для координаты и импульса. При этом нужно рассмотреть свет не в одной пространственной точке во все моменты времени, а во всем пространстве в один момент времени.

Любую волну можно представить, как суперпозицию плоских волн.  Рассмотрим выражение для фазы плоской волны любой природы:  ϕ= (k r, ) −ω ϕ⋅ +t ₀ = k x_x + k y_y + k z_z −ω ϕ⋅ +t ₀.

В это выражение произведение −ω⋅t входит, также как и произведение k x_x . Если свойства преобразования Фурье по временной координате t приводят к соотношению

           , то преобразование Фурье по пространственной координате x приведет к соотношению

          ∆k_x ⋅∆ ≥x .

           Умножим это соотношение на ℏ и получим

           .

          Рассмотрим импульс фотона

                                                     mc²               E ℏω ω

          p = mV = mc =        =    =        = ℏ = ℏk               =>      p = ℏk    =>

                                                        c       c       c         c

           p_x = ℏk_x .

   Тогда соотношение неопределенности для x координаты примет вид:

ℏ

          ∆p_x ⋅∆ ≥x               — это тоже соотношение неопределенности Гейзенберга

2

только для координаты и проекции импульса.

          Это соотношение справедливо не только для фотона, но и для любой