Интерполирование и аппроксимация функции. Геометрический смысл задач интерполяции. Интерполирование данных с помощью степенных полиномов

Министерство образования и науки РФ

НовосибирскИЙ государственнЫЙ УНИВЕРСИТЕТ экономики и управления

кафедра прикладных информационных технологий

Институт  Прикладной информатики

Учебная дисциплина:  Информационные технологии

ЛАБОРАТОРНАЯ РАБОТА № 3

Интерполирование и аппроксимация функции

Дисциплина:Информационные технологии

Номер группы:1741

Выполнил:  

Номер варианта:17

Проверила:

Дата регистрации на кафедре: «__»___________2013 г.

Интерполирование и аппроксимация функции

Аппроксимация функции заключается в приближённой замене функции f(х) некоторой функции g(x) так, чтобы отклонение было минимальным.

Функция g(х) называется аппроксимирующей.

Типичной задачей аппроксимации, является интерполяция.

Необходимость в интерполировании обусловлена причинами:

1.Функция f(x)  имеет сложное аналитическое решение, оказывающее трудности в её использовании.

2.Аналитческое описание функции неизвестно.

Функция f(x) задана таблично.

Постановка задач интерполяции на отрезке [a,b] заданы (n+1) точек х₀,х₁, х₂,..,х_n- узлы интерполяции.

Значение некоторой функции f(x₀):

f(x₀)=y₀; f(x₁)=y₁; f(x₂)=y₂;…f(x_n)=y_n

Геометрический смысл задач интерполяции заключается в том, что необходимо найти кривую, проходящую через точки (x_i,y_i).

Задача интерполяции решается однозначно, если вычислить поленом степени не выше n.

y=a₁x₁^n-1+a₂x₂^n-2+a₃x ₃^n-3

a₀, a₁- коэффициенты полинома.

Различают два вида интерполяции функции:

ü -Глобальная –соединения всех точек единым полиномом,

ü -Локальная – соединения всех точек отрезками, прямой (по 2 точкам).

Обзор полиноминальный функций:

1)  con v –умножение полинома,

2)  decon v- деление,

3)  poly – вычисление  полинома с заданными корнями,

4)  polyder-вычисление производных,

5)  polyfit-аппроксимация данных полинома,

6)  polyval-вычисление значения полинома в заданных точках,

7)  polyvalm- вычисление значений матричного полинома,

8)  residue- разложени на простые дроби,

9)  root- вычисление корней.

Задание 1. Интерполирование данных с помощью степенных полиномов.

Синтаксис функции polyfit.

p= polyfit(x,y,n)

1)  clc - очищаем командное окно

2) global var1;

3) global var2;       объявляем глобальные переменные

4) var1=[1.67 2.20;1.82 3.0;2.0 4.0;2.07 4.5;2.1 5.0;2.11 6.20;2.13 8.0]

5) var2=[1.94 3.0;2.13 4.0;2.25 6.0;2.32 7.0;2.4 11.0;2.46 15.0]

присваиваем значение переменной

6) x2=var1(:,1); -формирование вектора независимой переменной

7) y2=var1(:,2); -формирование вектора зависимой переменной

8) p2=polyfit(x2,y2,5)  - расчет  коэффициента полинома пятой степени

9) F2=polyval(P2,X2)  - вычисление значение полинома в заданных точках

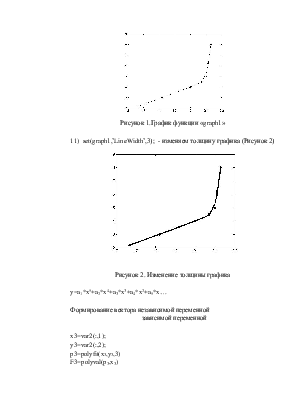
10) graph1=plot(x2,y2,’k*’,x2,y2,’k’);  -  строим график (Рисунок 1)

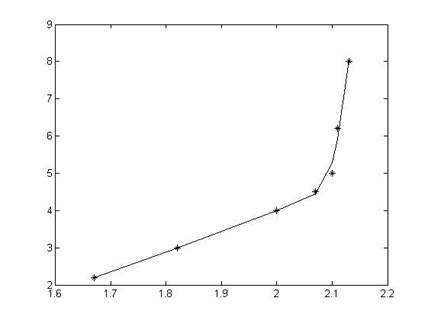
Рисунок 1.График функции «graph1»

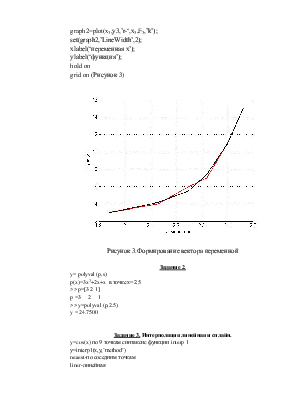
11)  set(graph1,’LineWidth’,3);  - изменяем толщину графика (Рисунок 2)

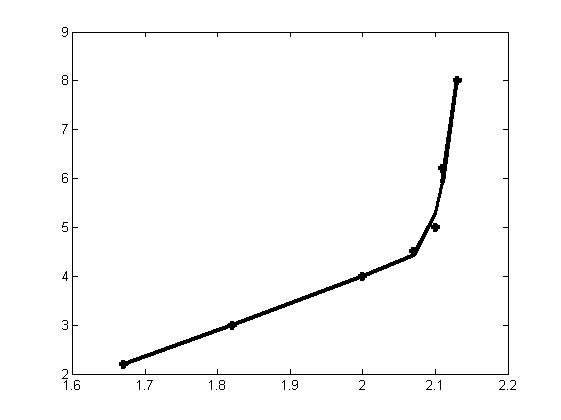
Рисунок 2. Изменение толщины графика

y=a₁*x⁵+a₂*x⁴+a₃*x³+a₄*x²+a₅*x…

Формирование вектора независимой переменной зависимой переменной

x3=var2(:,1);

y3=var2(:,2);

p3=polyfit(x₃,y₃,3)

F3=polyval(p₃,x₃)

graph2=plot(x₃,y3,’r-‘,x₃,F₃,’k’);

set(graph2,’LineWidth’,2);

xlabel(‘переменная x’);

ylabel(‘функция’);

hold on

grid on (Рисунок 3)

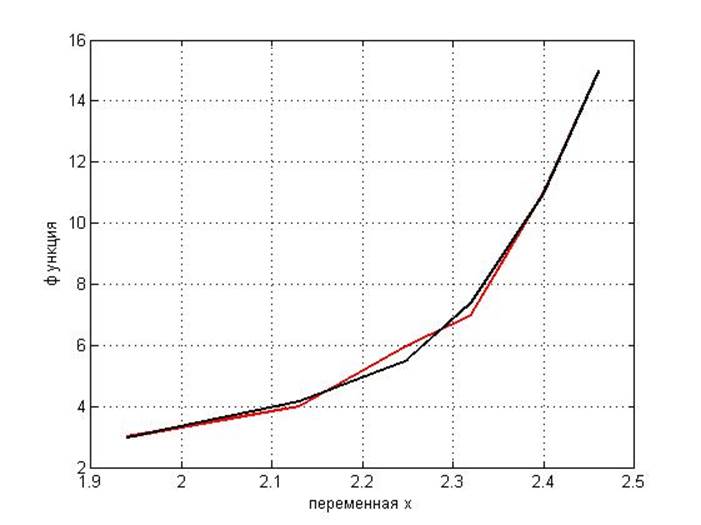
Рисунок 3.Формирование вектора переменной

Задание 2.

y= polyval (p,s)

p(x)=3x²+2x+x  в точке х=2.5

>> p=[3 2 1]

p =3     2     1

>> y=polyval (p,2.5)

y = 24.7500

Задание 3. Интерполяция линейная и сплайн.

y=cos(x) по 9 точкам синтаксис функции interp 1

y=interp1(x,y,’method’)

neaest-по соседним точкам

liner-линейная

spline-инт-я куб.сплайнами

cubic-кубич.полиномами

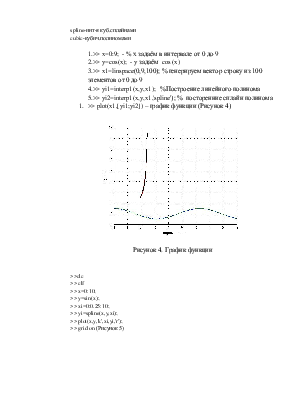
1.>> x=0:9;  - % х задаём в интервале от 0 до 9

2.>> y=cos(x);  - y задаём  cos (x)

3.>> x1=linspace(0,9,100); % генерируем вектор строку из 100 элементов от 0 до 9

4.>> yi1=interp1(x,y,x1);   %Построение линейного полинома

5.>> yi2=interp1(x,y,x1,'spline'); %  посторенние сплайн полинома

1.  >> plot(x1,[yi1;yi2]) – график функции (Рисунок 4)

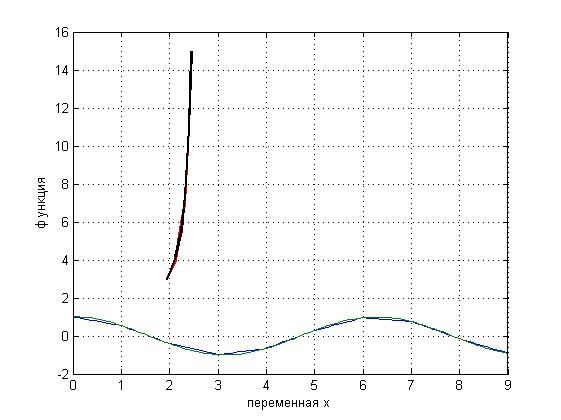
Рисунок 4. График функции

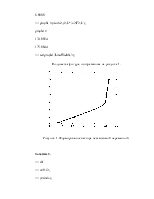
>>clc

>> clf

>> x=0:10;

>> y=sin(x);

>> xi=0:0.25:10;

>> yi=spline(x,y,xi);

>> plot(x,y,'k',xi,yi,'r');

>> grid on (Рисунок 5)

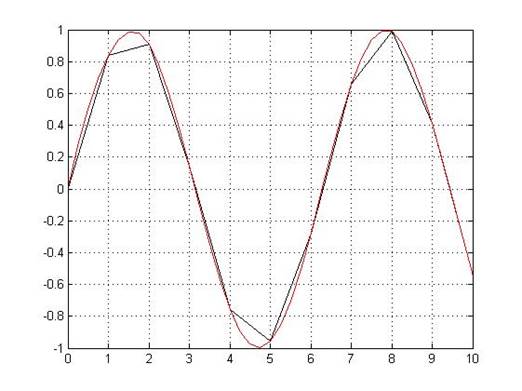
Рисунок 5.

>> clf

>> x=0:12;

>> y=exp(x)   % y=e^x

y =1.0e+005 *

0.0000    0.0000    0.0001    0.0002    0.0005    0.0015    0.0040    0.0110    0.0298    0.0810    0.2203    0.5987    1.6275

>> xi=0:0.08:15;

>> yi=spline(x,y,x_i);

>> plot(x,y,'k',x_i,y_i,'r');

>> grid on (Рисунок 6)

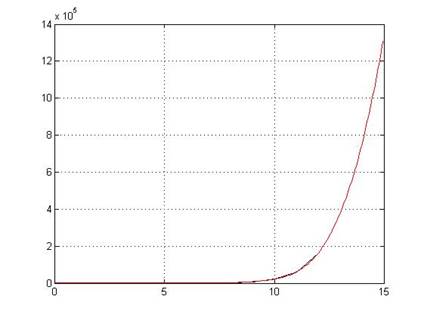
Рисунок 6.

Задание 4. Интерполяция табличных данных.

>> clf

>> x=[0.1       0.2       0.3       0.4       0.5       0.6       0.7       0.8       0.9]

>> y=[-2.99    -2.96   -2.91   -2.84   -2.75   -2.64   -2.57   -2.36   -2.19]

>> x_i=[x(1):0.1:x(length(x))];

>> ynear=interp1(x,y,x_i,'nearest');

>> yline=interp1(x,y,x_i,'spline');

>> subplot(2,2,1);