Информатика и выч. техника \ Информационные технологии управления персоналом

Интерполирование и аппроксимация функции. Геометрический смысл задач интерполяции. Интерполирование данных с помощью степенных полиномов, страница 2

>> plot(x,y,'k*');

>> title ('исходные данные'); (Рисунок 7)

>> subplot(2,2,2);

>> plot(x,y,'k*',xi,ynear,'k-');

>> title ('по соседним значениям'); (Рисунок 7)

>> subplot(2,2,3);

>> plot(x,y,'k*',xi,yline,'k-');

>> subplot(2,2,4);

>> plot(x,y,'k*',xi,yline,'k-');

>> title('кубический сплайн'); (Рисунок 7)

Рисунок 7.Интерполяция табличных данных.

Задание 5. Аппроксимация функции с помощью нейронных сетей.

Часто данные представляются в виде точек, координаты которых задаются таблично. В командном окне MatLab записывается код программы для создания и обучения сети.

A=zeros(1,20);

for i=1:20

A(i)=i*0.1;

End

T=[……]; % выходные значения.

Создание нейронной сети, вызов функции «new».

net=newff([-1 2.09],[5 1],{‘tansig’ ‘purelin’});

Функция newff создает «классическую» многослойную нейронную сеть с обучением по методу обратного распространения ошибки, т.е. изменения весов синапса, происходит с учетом функции ошибки.

Разница между полученными правильными ответами нейронной сети распространяется в обратном направлении. В примере сеть будет иметь два скрытых слоя. В первом слое пять скрытых  нейронов, во втором-один.

Функция активации первого слоя -  ‘tansig’,- это сигмоидальная функция возвращает в входные векторы в диапозоне от -1 до 1. Для второго слоя функция активации - ‘purelin’,- это линейная функция активации возвращает выходные векторы без изменения. В примере задано  50 эпох обучения. Для обучения нейронной сети используется функция ‘train’.

Задаём эпохи обучения:

net.trainParam.epochs = 50; потом обучаем сеть

net=train(net,P,T);

y=sim(net,P);

figure(1)

В результате обучения показывается график, на котором показывается время обучения и ошибка.

Самостоятельная работа.

Задание 1. Интерполирование данных с помощью степенных полиномов

>> var1 = [1.67  2.20; 1.82 3.0; 2.0 4.0; 2.07 4.50; 2.1 5.0; 2.11 6.20; 2.13 8.0]

var1 =

1.6700    2.2000

1.8200    3.0000

2.0000    4.0000

2.0700    4.5000

2.1000    5.0000

2.1100    6.2000

2.1300    8.0000

>>  var2= [1.94 3.00; 2.13  4.00;  2.25 6.00; 2.32 7.00; 2.4 11.0; 2.46 15.0]

var2 =

1.9400    3.0000

2.1300    4.0000

2.2500    6.0000

2.3200    7.0000

2.4000   11.0000

2.4600   15.0000

>> x2=var1(:,1);

>> y2=var1(:,2);

>> P2=polyfit(x2,y2, 6)

P2 =  1.0e+009 *

-0.0054    0.0632   -0.3105    0.8119   -1.1924    0.9324   -0.3033

Задание 2. Вычислить значения полинома в заданной точке

>> var1 = [1.67  2.20; 1.82 3.0; 2.0 4.0; 2.07 4.50; 2.1 5.0; 2.11 6.20; 2.13 8.0]

>>  var2= [1.94 3.00; 2.13  4.00;  2.25 6.00; 2.32 7.00; 2.4 11.0; 2.46 15.0]

>> x2=var1(:,1);

>> y2=var1(:,2);

>> P2=polyfit(x2,y2, 6)

P2 =  1.0e+009 *

-0.0054    0.0632   -0.3105    0.8119   -1.1924    0.9324   -0.3033

>> F2=polyval(P2,x2)

F2 =  2.2000

3.0000

4.0000

4.5000

5.0000

6.2000

8.0000

>> graph1 = plot(x2,y2,'k*',x2,F2,'k');

graph1 =

174.0054

175.0044

>> set(graph1,'LineWidth',3);

Получается фигура, изображённая на рисунке 1.

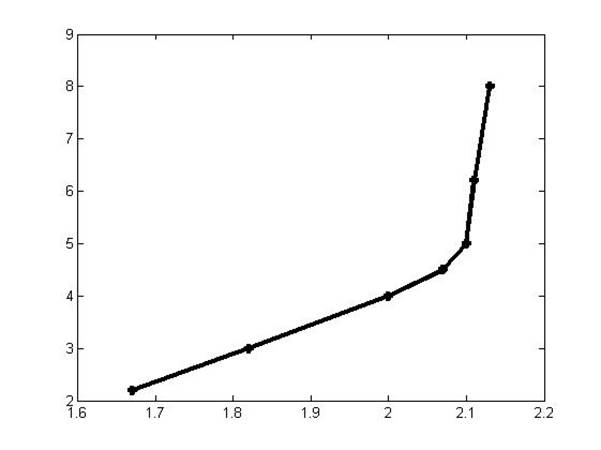
Рисунок 1 .Формирование вектора независимой переменной.

Задание 3.

>> clf

>> x=0:12;

>> y=sin(x);

>> xi=0:0.17:12;

>> yi=spline(x,y,xi);

>> plot(x,y,'k',xi,yi,'r');

>> grid on            (Рисунок 2)

Рисунок 2.

>> clf

>> x=0:12;

>>  y=sin(x);

>> x=0:12;

>>  clf

>> x=0:12;

>> y=cos(x);

>>  xi=0:0.17:12;

>> yi=spline(x,y,xi);

>>  plot(x,y,'k',xi,yi,'r');

>> grid on (Рисунок 3)

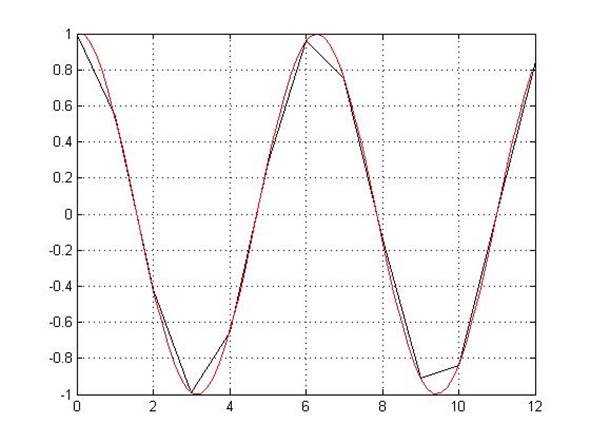
Рисунок 3.

>> clf

>> x=0:12;

>> y=tan(x);

>> xi=0:0.17:12;

>> yi=spline(x,y,xi);

>>  plot(x,y,'k',xi,yi,'r');

>> grid on (Рисунок 4 )

Рисунок 4.

Задание 4. Интерполяция табличных данных

Y=Y+0.08*N

X

0.010

0.020

0.030

0.040

0.050

0.060

0.070

0.080

0.090

Y

1.480

1.479

1.478

1.477

1.475

1.473

1.470

1.467

1.464

Y(Y+0.08*N)

2.84

2.839

2.838

2.837

2.835

2.833

2.83

2.827

2.824

Решение:

Y=Y+0.08*N

N=17, 0.08*17=1.36,

>> clf

>> x=[0.010,0.020,0.030,0.040,0.050,0.060,0.070,0.080,0.090]

x =0.0100    0.0200    0.0300    0.0400    0.0500    0.0600    0.0700    0.0800    0.0900

>> y=[2.84,2.839,2.838,2.837,2.835,2.833,2.83,2.827,2.824]

y = 2.8400    2.8390    2.8380    2.8370    2.8350    2.8330    2.8300    2.8270    2.8240

>> xi=[x(1):1.36:x(length(x))];

>> ynear=interp1(x,y,xi,'nearest');

>> yline=interp1(x,y,xi,'spline');

>> subplot(2,2,1);

>> subplot(2,2,1);

>> plot(x,y,'k*');

>> title('исходные данные'); (Рисунок 5)

>> subplot(2,2,2);

>> plot(x,y,'k*',xi,ynear,'k-');

>> title('По соседним значениям'); (Рисунок 5)

>> subplot(2,2,3);

>> plot(x,y,'k*',xi,yline,'k-');

>> subplot(2,2,4);

>> plot(x,y,'k*',xi,yline,'k-');

>> title('кубический сплайн'); (Рисунок 5)

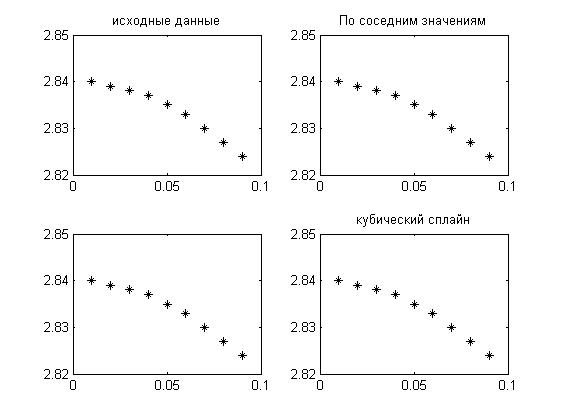
Рисунок 5.

Скачать файл