






МПС РФ
Петербургский Государственный
Система автоматического управления
температурой в салоне пассажирского
вагона.
Степанов С.В.
Проверила: Жарова Е.А.
Санкт-Петербург
2004
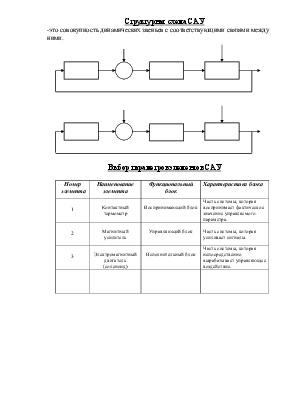
Элемент (группа элементов), выполняющих одну и ту же функцию, называется функциональным блоком. Совокупность функциональных блоков с соответствующими связями между ними называется функциональной схемой.
![]()
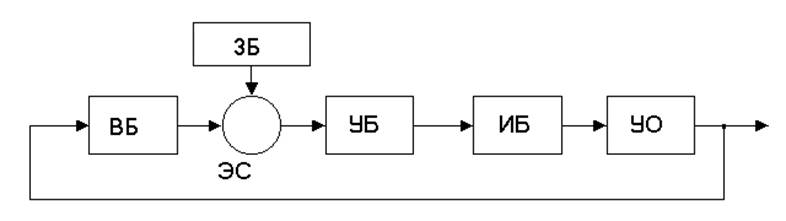
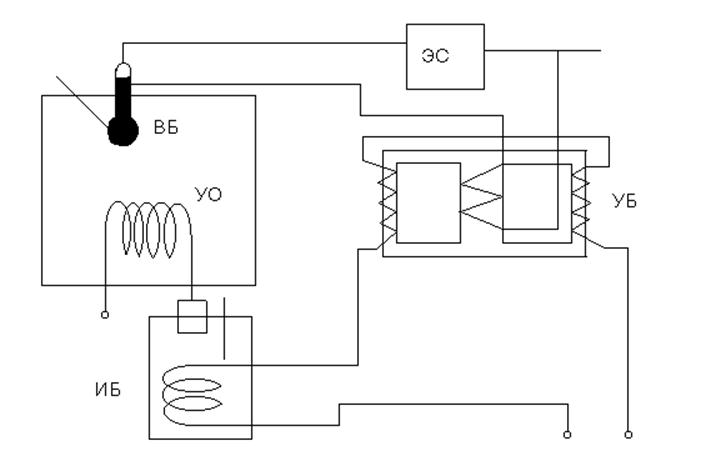
ВБ - воспринимающий блок;
ЗБ - задающий блок;
ЭС - элемент сравнения;
УБ - управляющий блок;
ИБ - исполнительный блок;
УО - управляемый объект;
![]() -
возмущающее воздействие;
-
возмущающее воздействие;
![]() -
управляемый параметр;
-
управляемый параметр;
![]() -
контрольное воздействие
-
контрольное воздействие
Принципиальная схема системы
автоматического управления температурой
в салоне пассажирского вагона
Структурная схема САУ
-это совокупность динамических звеньев с соответствующими связями между ними.
 |
|||||||||
 |
|||||||||
 |
|||||||||
 |
|||||||||
 |
|||||||||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Номерэлемента |
Наименование элемента |
Функциональный блок |
Характеристика блока |
|
1 |
Контактный термометр |
Воспринимающий блок |
Часть системы, которая воспринимает фактическое значение управляемого параметра. |
|
2 |
Магнитный усилитель |
Управляющий блок |
Часть системы, которая усиливает сигналы. |
|
3 |
Электромагнитный двигатель (соленоид) |
Исполнительный блок |
Часть системы, которая непосредственно вырабатывает управляющее воздействие. |
|
Эле-мент |
Динамическое звено |
Шифр звена |
Уравнение передаточной функции W(S) |
Принятые параметры уравнения
|
|
1 |
Инерционное |
ВБ |
|
0,1 60 |
|
2 |
Инерционное |
УБ |
|
40 0,25 |
|
3 |
Колебательное |
ИБ |
|
2 0,25 0,5 |
Уравнение математической модели САУ
с использованием передаточной функции:
![]() ,
,
где
![]() - переходная функция разомкнутой
системы:
- переходная функция разомкнутой
системы:
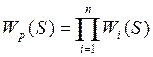 ,
,
![]() -
передаточная функция i-го звена
-
передаточная функция i-го звена
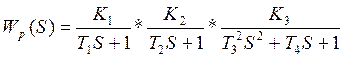 ;
;
![]() ;
;
![]() - передаточная
функция возмущающего воздействия.
- передаточная
функция возмущающего воздействия.
Тогда уравнение САУ можно переписать в виде:
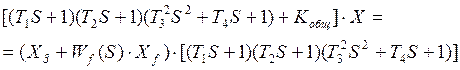
Рассмотрим выражение в квадратных скобках, приравняв его к 0:
![]()
После преобразования получим:
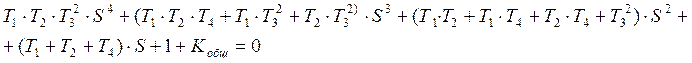
Используя данные таблицы, имеем:
![]()
Устойчивость САУ
Устойчивостью называют способность системы возвращаться в исходное состояние равновесия после снятия с нее возмущения, которое вывело систему из этого равновесия. Основным условием устойчивости системы является:
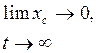
где
![]() - собственное движение системы.
- собственное движение системы.
Критерии устойчивости
1. Критерий Гурвица
Применяется для уравнений не выше 6-го порядка.
![]()
![]()
![]()
![]() Составляется
главный определитель Гурвица, в который по главной диагонали вписываются коэффициенты
уравнения, начиная с а . Затем заполняются столбцы: вверх по возрастающим
индексам, вниз – по убывающим. Если индекс меньше 0 или больше n, то
записывается 0. После этого выделяется соответствующий определитель:
Составляется
главный определитель Гурвица, в который по главной диагонали вписываются коэффициенты
уравнения, начиная с а . Затем заполняются столбцы: вверх по возрастающим
индексам, вниз – по убывающим. Если индекс меньше 0 или больше n, то
записывается 0. После этого выделяется соответствующий определитель:
![]() D=
D= 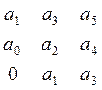 =
= 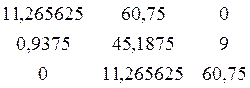
Вычислим определитель третьего порядка:
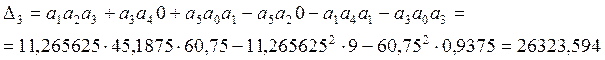
Получаем:
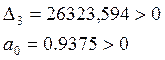
Система устойчива по критерию Гурвица.
2. Критерий Михайлова
Построим кривую Михайлова (годограф)
Рассмотрим характеристическое уравнение D(S)
![]() ;
;
Заменим S на iw:
![]()
Вычислим действительную и мнимую части уравнения, считая, что
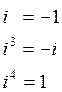
Рассмотрим последнее выражение в виде:
![]()
![]()
![]()
Построим график полученных функций
|
Круговая частота w |
X(w) |
Y(w) |
|
0 |
9 |
0 |
|
1 |
-35.25 |
49.48 |
|
2 |
-156.75 |
31.38 |
|
3 |
-321.75 |
-121.92 |
|
4 |
-474 |
-478 |
|
5 |
-534.75 |
-1104.45 |
|
6 |
-402.75 |
-2068.88 |
|
7 |
45.75 |
-3438.86 |
|
8 |
957 |
-5282 |
|
9 |
2499.75 |
-7665.89 |
|
10 |
4865.25 |
-10658.13 |
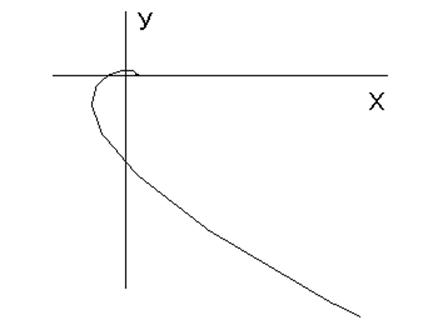
По критерию Михайлова система устойчива, т.к. кривая Михайлова проходит плавно против часовой стрелки столько квадрантов (П/2), какова степень характеристического уравнения, т.е. 4 и уходит в бесконечность.
Оценка качества системы
1. Запас устойчивости
1.1 Максимальное значение управляемой величины:
![]()
1.2 Динамический заброс:
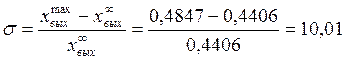 %
%
Динамический заброс соответствует нормальной системе.
1.3 Число колебаний:
![]() - соответствует нормальной системе.
- соответствует нормальной системе.
1.4 Затухание по корню ![]() :
:
![]() ,
,
где ![]() - действительная часть корня
- действительная часть корня ![]() ,
,
![]() ;
;
![]() - мнимая часть корня
- мнимая часть корня ![]() ,
, ![]() ;
;
![]()
Затухание имеет значение, превышающее нормальное. Для сдемпфированных систем значение затухания находится в
пределах от 0,9 до 0,98.
1.5 Колебательность (склонность системы колебаться) по
корню ![]() :
:
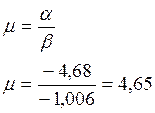
Показатель колебательности характеризует высоту резонансного пика амплитудно-частотной характеристики. Колебательность имеет значение, превышающее нормальное. Для нормально сдемпфированных систем – 1,52….2,72.
1.6 Запас устойчивости по амплитуде и по фазе.
Эти показатели отражают особенности критерия устойчивости Найквиста. Запас устойчивости по амплитуде представляет собой удаление годографа частотно-передаточной функции разомкнутой системы от точки (-1;0) по действительной оси при фазе – п.
![]()
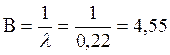
![]()
Показатель запаса устойчивости по фазе превышает нормальное значение в пределах от 30 до 60.
2. Показатели быстродействия
2.1 Время переходного процесса:
![]()
![]()
Чем меньше время, тем быстродействие выше.
2.2 Средний геометрический корень:
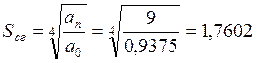
2.3 Степень быстродействия
За степень быстродействия принимают абсолютное значение действительной части ближайшего к мнимой оси корня характеристического уравнения. Этот корень соответствует наиболее медленно затухающей составляющей переходного процесса.
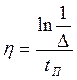 ;
; ![]()
Методы и средства корректировки качества
автоматического управления.
1. Повышение точности автоматического управления.
Одним из методов повышения точности является увеличение коэффициента передачи разомкнутой системы, но это значительно снижает запас устойчивости.
2. Повышение запаса устойчивости:
а) путь параметрического изменения системы (К и Т);
б) путь структурного изменения системы (методом ввода корректирующего звена).
3. Повышение быстродействия
а) путем параметрического изменения системы;
б) ввод корректирующего звена.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.