Типовые звенья САР. Определение. Классификация звеньев. Классификация типовых линейных звеньев

Физически апериодическое звено содержит один накапливающий энергию элемент, а также один или несколько элементов способных ее рассеивать.

Из уравнения (3.8) следует, что передаточная функция апериодического звена равна:

(3.9)

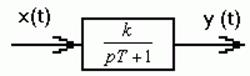
Рис.3.9 - Представление апериодического звена на структурных схемах

Знаменатель передаточной функции (3.9) называется характеристическим полиномом апериодического звена:

(3.10)

Приравнивание характеристического полинома к нулю дает характеристическое уравнение апериодического звена:

(3.11)

pT + 1 = 0

Его решения называются корнями характеристического полинома. В данном случае корень один:

(3.12)

Этот корень и определяет инерционные свойства апериодического звена.

Комплексный коэффициент передачи апериодического звена следует из (3.9):

(3.13)

ЛАЧХ и ЛФЧХ апериодического звена получаются из (3.13): (3.14)

Рис.3.10 - ЛАЧХ и ЛФЧХ двух апериодических звеньев с коэффициентами усиления 22 (27 дБ) и 8 (18 дБ) и постоянными времени, равными 1 сек и 0.1 сек, и кусочно-линейно аппроксимация ЛАЧХ первого звена. Коэффициент усиления звена k определяет уровень ЛАЧХ в низкочастотной области, постоянная времени Т определяет частоту точки сопряжения линейных участков аппроксимации ЛАЧХ. На частоте 1/Т задержка по фазе апериодического звена составляет – 45⁰. ЛФЧХ апериодического звена равна нулю на нулевой частоте, а с увеличением частоты стремится к -90⁰

Переходная характеристика апериодического звена может быть получена обратным преобразованием Лапласа передаточной функции: (3.15)

или непосредственным решением дифференциального уравнения (3.8)

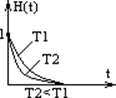
Рис. 3.11 - Примеры переходных характеристик апериодических звеньев. Коэффициент усиления звена определяет уровень, к которому стремится переходная характеристика с течением времени. Касательная, проведенная в начале координат к переходной характеристике, пересекает этот уровень в момент времени, равный постоянной времени апериодического звена Т. Эти свойства апериодического звена, а также то, что переходный процесс заканчивается приближенно за время, равное 3Т, позволяет определять параметры звена (коэффициент усиления и постоянную времени) по его экспериментальной переходной характеристике

Апериодическое звено не сразу, а постепенно реагирует на ступенчатое воздействие, в этом и проявляется его инерционность, которая численно может характеризоваться величиной постоянной времени, поскольку переходный процесс заканчивается примерно за 3Т. За время 3Т переходная характеристика достигает 95% уровня, к которому она стремиться при стремлении времени к бесконечности.

Примеры апериодических звеньев:

                   а) Термопара         x=t⁰  →y = термо ЭДС.

                  б) Двигатель постоянного тока.  x=Iя →y = скорость вращения.

                  в) Тепловой двигатель    x = подача топлива → y =скорость вращения.

                  г) Корректирующая LR цепь

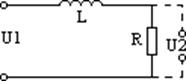
Рис. 3.12

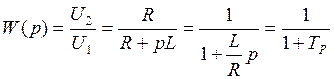
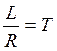 - постоянная времени цепи

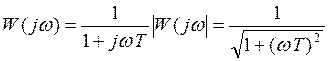                                           - АЧХ

argW(jω) = -arctgωT          -  ФЧХ

H(t) = k(1-e^-t/T)    – ПХ

3.3.2 Форсирующее звено (ускоряющее звено)

В чистом виде, автономно форсирующее звено в природе не существует. Автономно оно физически не реализуемо, но может быть включено как элемент в модели более сложных звеньев и широко применяется в практике построения систем управления.

Форсирующее звено при правильно подобранных параметрах стабилизирует систему и одновременно повышает ее быстродействие.

 Форсирующее звено – это такое, у которого передаточная функция равна:

Как видно передаточная функция обратна передаточной функции инерционного звена, поэтому включение форсирующего звена последовательно с инерционным уменьшает их общую инерционность.

Пример: ПИ-регулятор, устройство, задающее закон регулирования, часто используемый на практике. Его передаточная функция содержит форсирующий множитель:

3.3.3 Дифференцирующие звенья

3.3.3.1  Идеальное дифференцирующее звено

     Звено описывается уравнением  y=к*dx/dt  или, в операторной форме

y=кpx

     Такое звено в природе не существует, но ряд устройств по своим  свойствами очень близки к идеальному дифференцирующему звену.

Примеры: 1 Дифференциатор на 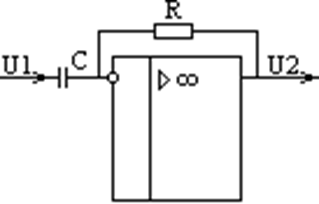ОУ.

Его выходное напряжение

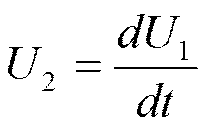
                   2: Тахогенератор. Это генератор, выходное напряжение которого пропорционально скорости вращения вала ,то есть производной от угла поворота.

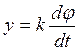
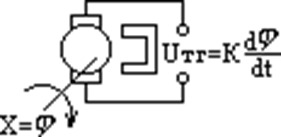
Представим в операторной орме, тогда

y=px

;

3.3.3.2 Инерционно - дифференцирующее звено

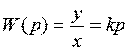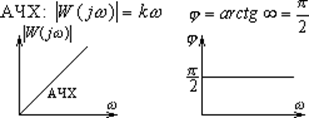
Такие звенья применяются в так называемых гибких обратных связях, повышая при правильно подобранных параметрах, быстродействие и устойчивость 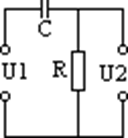системы

Инерционно-дифференцирующее звено это такое, передаточная функция которого равна:

. Примеры :

1) Дифференцирующая RCцепь

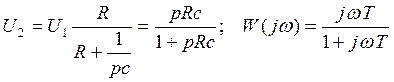
RC=T-постоянная времени.

                                     АЧХ: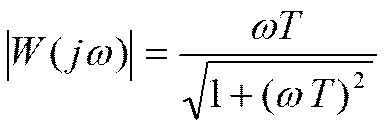           

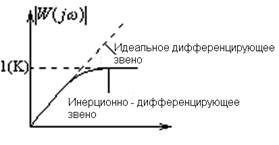
                                   ФЧХ: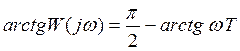                                             

                                   ПХ::                                                                                     

          2) Цилиндр, заполненный жидкостью, связанный с пружиной. В нем перемещается поршень с отверстием, через которое перетекает