Криволинейный интеграл по ломаной АВС. Вычисление криволинейного интеграла. Поверхностный интеграл по указанной поверхности

Варианты заданий

Вариант 1

1.  Вычислить криволинейный интеграл по ломаной АВС:

 А(-1/3, -4), В(-1/3, 1), С(1, 2).                                                                                         (50)

2.  Вычислить криволинейный интеграл:

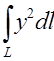, L: x=R cos t, y=R sin t (0≤t≤π).                                                                                                (π R³/2)

3.  Вычислить криволинейный интеграл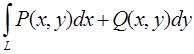 по кривой L между точками A и B:

, L: y=3x²/10, A(0, 0), B(2, 6/5).                                                                             ()

4.  Вычислить криволинейный интеграл  по заданной линии L:

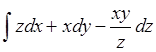; L: x=t cos t, y=t sin t, z=t, 0≤t≤π/2.                                                                         (π/4-1)

5.  Найти работу, производимую силой F=(P, Q, R) вдоль пути L:

F=(y-x,xz,x²), L: прямая от А(0, 2, -1) до В(2, 1, 0).                                                                               (17/3)

6.  Вычислить криволинейный интеграл  между точками А и В по различным путям интегрирования С₁ (отрезок АВ) и С₂ и обосновать полученные результаты, используя условие независимости криволинейного интеграла от пути интегрирования:

P= x+y, Q= -x, A(0, 0), B(4, 2), C(2, 0); C₂: ломаная АСВ.                                                                       (8;4)

7.  Вычислить криволинейный интеграл , применив формулу Грина (обход контура L оставляет область, ограниченную контуром, слева):

P= (1-x²)y, Q=x(1+y²); L: x²+y²=R² .                                                                                                 (πR⁴/2)

8.  Вычислить поверхностный интеграл  по поверхности G:

F=x²+y+z²-2, G – часть поверхности 2y=9-x²-z², отсеченная плоскостью y=0.

(π(500-23)/15)

9.  Вычислить поверхностный интеграл по указанной поверхности:

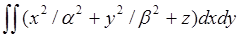; G – внешняя сторона части поверхности z=c²-x²/α²-y²/β², отсеченной плоскостью z=0.                                                                                                                                  (πabc⁴)

10.  Вычислить площадь поверхности S:

S: 2x+2y-z=1, вырезанная цилиндром x²+y²=1.                                                                                           (3π)

11.  С помощью формулы Гаусса-Остроградского вычислить поверхностный интеграл второго рода 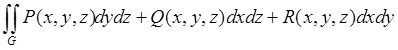по внешней стороне замкнутой поверхности G:

P=x³, Q=y³, R=z³; G: x+y+z=2, x=0, y=0, z=0.                                                                                         (4,8)

12.  Вычислить криволинейный интеграл по контуру L, применяя формулу Стокса:

P=y+z, Q=z+x, R=x+y; L:x²+y²+z²=α², x+y+z=0.                                                                                      (0)

Вариант 2

1.  Вычислить криволинейный интеграл по ломаной АВС:

; А(-4, 0), В(0, 0), С(4, 2).                                                                                               ()

2.  Вычислить криволинейный интеграл:

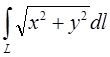, L – верхняя половина кардиоиды .                                                       (16α²/3)

3.  Вычислить криволинейный интеграл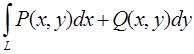 по кривой L между точками A и B:

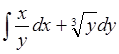, L: y=x³, A(1, 1), B(2, 8).                                                                                            (11,75)

4.  Вычислить криволинейный интеграл  по заданной линии L:

 L: x=α ch t, y=α sh t, z=bt, .                                                             (α²(b-1))

5.  Найти работу, производимую силой F=(P, Q, R) вдоль пути L:

F=(z³, x, y²), L: x=t³, y=t², z=t, .                                                                                                (1,1)

6.  Вычислить криволинейный интеграл  между точками А и В по различным путям интегрирования С₁ (отрезок АВ) и С₂ и обосновать полученные результаты, используя условие независимости криволинейного интеграла от пути интегрирования:

P=x²y, Q=x³/3, A(-1, 0), B(0, 2); C₂: y²=4(x+1).                                                                                      (0)

7.  Вычислить криволинейный интеграл , применив формулу Грина (обход контура L оставляет область, ограниченную контуром, слева):

P=x+y, Q=-(x-y); L: x²/α²+y²/b²=1.                                                                                                        (-2παb)

8.  Вычислить поверхностный интеграл  по поверхности G:

F=, G – часть поверхности z=, вырезанная цилиндром x²+y²=2x.

(3π)

9.  Вычислить поверхностный интеграл по указанной поверхности:

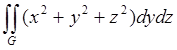; G – внутренняя сторона части поверхности x=, отсеченной плоскостями x=0, x=α.                                                                                                                                             (πα⁴)

10.  Вычислить площадь поверхности S:

S: z=x²+y², отсеченная плоскостью z=2.                                                                                            (13π/3)

11.  С помощью формулы Гаусса-Остроградского вычислить поверхностный интеграл 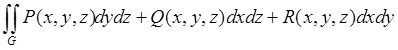по внешней стороне замкнутой поверхности G:

P=Q=R= G: x²+y²+z²=R².                                                                                                    (0)

12.  Вычислить криволинейный интеграл по контуру L, применяя формулу Стокса:

P=y-z, Q=z-x, R=x-y; L:x²+y²=1, x+z=1.                                                                                                 (-4π)

Вариант 3

1.  Вычислить криволинейный интеграл по ломаной АВС:

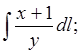 A(-2, -2), B(0, 2), C(3, 2).                                                                               (15/4+)

2.  Вычислить криволинейный интеграл:

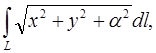 L – дуга спирали Архимеда  между точками A(0,0) и B(a,1).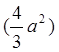                    

3.  Вычислить криволинейный интеграл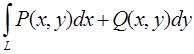 по кривой L между точками A и B:

                                                                                 

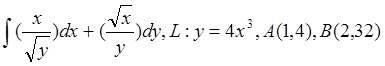
4.  Вычислить криволинейный интеграл  по заданной линии L:

 L: x=α cos t, y=α sin t, z=t, .                                                           (πα²)

5.  Найти работу, производимую силой F=(P, Q, R) вдоль пути L:

F=(-yz/x, x, y), L :x=t, y=tcost, z=tsint,                                                                     

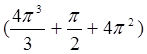
6.  Вычислить криволинейный интеграл  между точками А и В по различным путям интегрирования С₁ (отрезок АВ) и С₂ и обосновать полученные результаты, используя условие независимости криволинейного интеграла от пути интегрирования:

P=-xy², Q=2xy, A(0,1), B(2,3); C₂: y=x²/2+1.                                                                                    (0;46/15)                                                            

7.  Вычислить криволинейный интеграл , применив формулу Грина (обход контура L оставляет область, ограниченную контуром, слева):

.                                                                                (0)

8.  Вычислить поверхностный интеграл  по поверхности G:

F=, G – часть поверхности x=, вырезанная цилиндром              (y-1)²+z²=1.                                                                                                                                  (9π)

9.  Вычислить поверхностный интеграл по указанной поверхности:

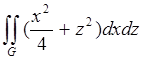; G – внутренняя сторона части поверхности y=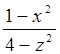, отсеченной плоскостями y=0.                                                                                                                         (-π)

10.  Вычислить площадь поверхности S:

S: z/2+x-y+5=0, вырезанная цилиндром x²+y²/4=1.                                                                              (6π)

11.  С помощью формулы Гаусса-Остроградского вычислить поверхностный интеграл 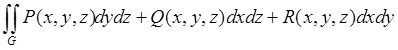по внешней стороне замкнутой поверхности G:

P=x³, Q=y³, R=z³;  G: x²+y²+z²=1.                                                                                                       (2,4 π)

12.  Вычислить криволинейный интеграл по контуру L, применяя формулу Стокса:

P=x, Q=x+y, R=x+y+z; L:x=asint, y=acost, z=a(sint+cost), .                                                      (-πa²)

Вариант 4

1.  Вычислить криволинейный интеграл по ломаной АВС:

 A(0, -5), B(0, 1), C(4, 4).                                                                                                 (30)

2.  Вычислить криволинейный интеграл:

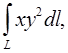L-первая четверть окружности: x=R*cos(t), y=R*sin(t).                 (R⁴/3)

3.  Вычислить криволинейный интеграл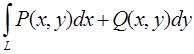 по кривой L между точками A и B:

                                                                                        

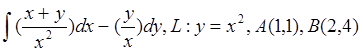
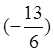
4.  Вычислить криволинейный интеграл  по заданной линии L:

 L: x=sin t, y=sin² t, z=sin³ t, .                                                       (1,9)

5.  Найти работу, производимую силой F=(P, Q, R) вдоль пути L:

F=(yz, xz, xy), L: x=t², y=t⁴, z=t⁶,                                                                                                  (1)

6.  Вычислить криволинейный интеграл  между точками А и В по различным путям интегрирования С₁ (отрезок АВ) и С₂ и обосновать полученные результаты, используя условие независимости криволинейного интеграла от пути интегрирования:

P=y/x, Q=lnx, A(1,1), B(e,e), c(0,1); C₂: ломанная АСВ.                                                                           (e)                                                                          

7.  Вычислить криволинейный интеграл , применив формулу Грина (обход контура L оставляет область, ограниченную контуром, слева):

P=xy+x+y, Q=xy+x-y; L: x²/α²+y²/b²=1.                                                                                                             (0)

8.  Вычислить поверхностный интеграл  по поверхности G:

F=y(x+z), G – часть поверхности y=,отсеченная плоскостями x=0, x=1.                                        (1)

9.  Вычислить поверхностный интеграл по указанной поверхности:

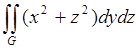; G – внешняя сторона части поверхности x=, отсеченной плоскостями