Для уравнений, в которых n£5 более простая формулировка: чтобы все корни характеристического уравнения имели отрицательные вещественные части необходимо и достаточно, чтобы все коэффициенты этого уравнения и определитель Dn-1 были положительными. Отсюда следуют условия устойчивости:
Уравнение 1-го порядка: а>0, а0>0
2-го порядка: а2>0, а1>0, а0>0 ;
3-го порядка: а3>0, а2>0, а1>0, а0>0 и D2>0, т.е. а1× а2 – а0× а3 >0;
4-го порядка: аi>0 и D3>0;
5-го порядка: аi>0 и D4>0.
При n>5 определители очень громоздкие и критерий не используется.
Пример: Исследуем на устойчивость систему с характеристическим уравнением (5.1).В этом случае аi>0 ,но D3 отрицательно.
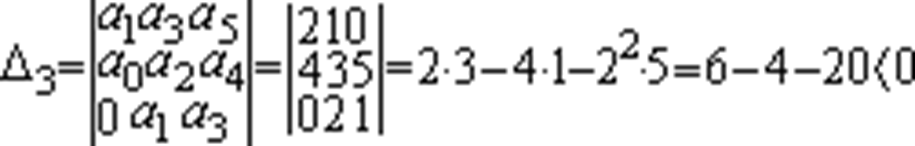
Значит, система с таким характеристическим уравнением неустойчива.
Исследуем на устойчивость фотоэлектрическую систему слежения (ФСС).Ее характеристический полином
Так как система 3-го порядка, то необходимо исследовать определитель 2-го порядка.
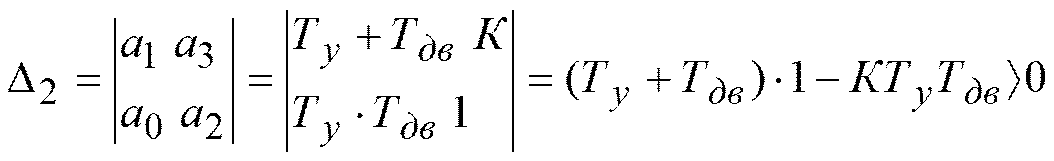 ,где К=К1К2К3К4.
,где К=К1К2К3К4.
Отсюда 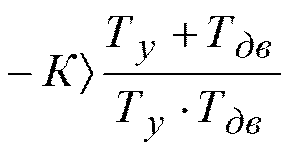 ;
;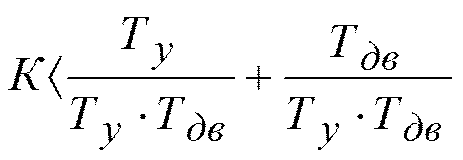
Поэтому необходимое и достаточное условие устойчивости
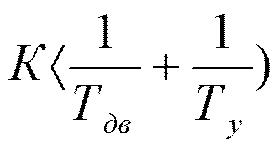 .
.
Данное неравенство показывает, что инерционное запаздывание усилителя и двигателя неблагоприятно влияет на устойчивость. Чем больше Ту или Тдв ,тем ближе система к колебательной границе устойчивости
5.3.2 Критерий устойчивости Михайлова
Рассмотрим
характеристический полином 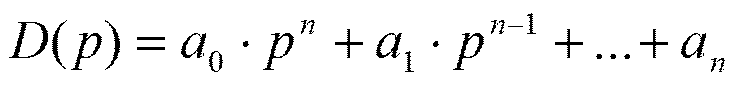 . Подставим
. Подставим 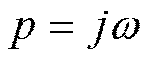 , тогда получим
характеристический комплекс
, тогда получим
характеристический комплекс 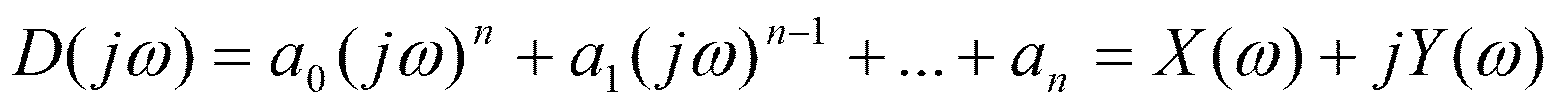 .
.
Здесь ![]() содержит чётные
степени w, а
содержит чётные
степени w, а ![]() - нечётные степени.
- нечётные степени.
Если значение w менять непрерывно от 0 до бесконечности, то вектор D(jw)
опишет своим концом кривую (годограф) Михайлова. Для устойчивости
системы необходимо и достаточно, чтобы вектор D(
jw) при изменении w от 0 до ¥
повернулся на угол 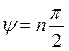 против часовой стрелки, нигде не
меняя направления поворота.
против часовой стрелки, нигде не
меняя направления поворота.
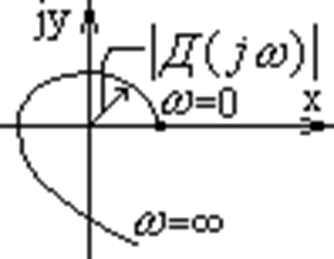
Годограф Михайлова
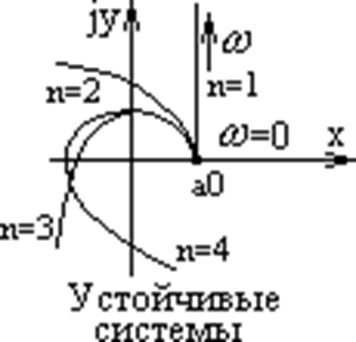
Годографы Михайлова для устойчивых и неустойчивых систем различного порядка.
Для системы 1-го
порядка D(р)=а1р+а0 ; D(jw) =a0+ja1w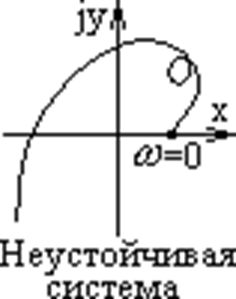
 кривая Михайлова
вырождается в прямую.
кривая Михайлова
вырождается в прямую.
С помощью критерия Михайлова исследуем устойчивость системы с характеристическим полиномом, D(р)=4р4+2р3+3р2+р+5=0 рассмотренным по критерию Гурвица .
D(jw) =4w4-2jw3-3w 2+jw+5; х(w)=4w4-3w2+5; у(w)=-2w3+w.
Из условия у(w)=0 найдем частоту ,на которой кривая пересекает ось х.
-2w3+w=0;отсюда
w1=0, или -2w3=-1; ![]() ; х(w1)=5 .Поэтому координаты точек пересечения А(5;0); х(w2)=4,5 В(4,5;0)
; х(w1)=5 .Поэтому координаты точек пересечения А(5;0); х(w2)=4,5 В(4,5;0)
Из условия х(w)=0 ищем точки пересечения кривой с осью у. 4w4-3w2+5=0;отсюда w2=z; 4z2-3z+5=0 Определитель ∆=9-80=-71, – вещественных корней нет. Значит кривая Михайлова не имеет точек пересечения с осью ординат. Кривая не прошла через 4 четверти и вектор менял направление поворота, поэтому система неустойчива.
Критерий Найквиста
Критерий Найквиста позволяет судить об устойчивости замкнутой системы автоматического управления по амплитудно - фазовой характеристике разомкнутой системы.
Для этого в выражение передаточной функции разомкнутой системы подставляют p=jw
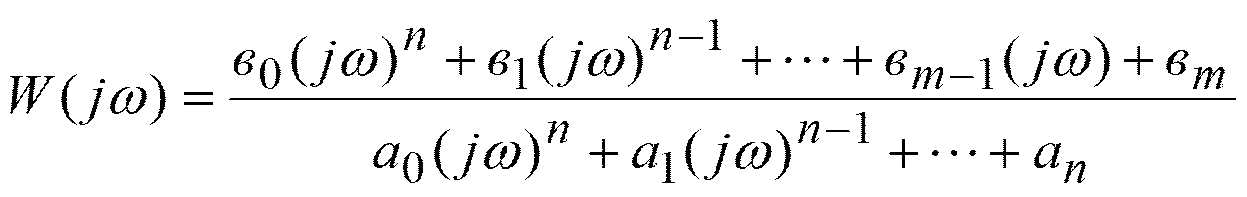 Придается
значение w от 0 до ¥ и строится годограф вектора W(jw)
,который и представляет АФХ.
Придается
значение w от 0 до ¥ и строится годограф вектора W(jw)
,который и представляет АФХ.
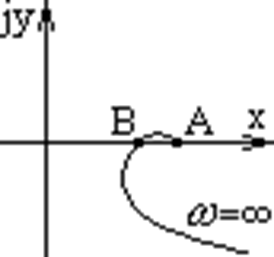
Замкнутая система устойчива, если АФХ устойчивой разомкнутой системы не охватывает точку с координатами (-1; j 0) при изменении w от 0 до ¥.
1. Годограф Найквиста спиралевиден.
2. При ω→∞ годограф W(jω)→0, т.к. нет безынерционных систем.
3. Годограф статических САР начинается из точки на вещественной оси.
4. Для положительных и отрицательных частот годографы зеркально симметричны относительно оси х
5. Наличие корней на границе устойчивости приводит к устремлению годографа в ∞ и приращению его фазы на -180°.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.