Устойчивость линейных САУ. Основные понятия устойчивости. Решение линейного дифференциального уравнения для переходного процесса

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                 Глава 5 – Устойчивость линейных САУ                                                                                      

5.1 Основные понятия устойчивости

Значение управляемой величины системы y(t) в  каждый момент времени может быть представлено в виде суммы установившейся и переходной составляющих.

y(t)= y_уст.(t)+ y_перех.(t).

САУ считается устойчивой, если  (асимптотическая устойчивость). Иногда рассматривается техническая устойчивость (устойчивость в малом), если 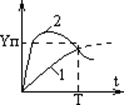управляемая величина у не превосходит заданной величины при 0 £t£T

1 – технически устойчивая САУ

2 – технически неустойчивая САУ                 

           Решение линейного дифференциального уравнения для переходного процесса имеет вид: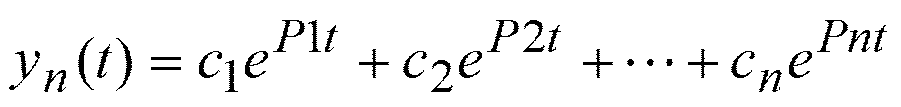                                                    

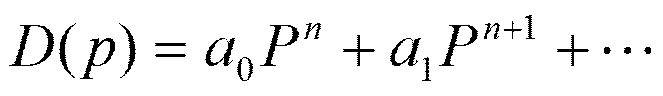
Условие устойчивости выполняется лишь в том случае, когда каждая из экспоненциальных составляющих стремится к 0. Если корень вещественный p_i = a_i ,      то a_i должно быть обязательно < 0. Если корни комплексные p_i;i+1 = a_i±jb_i  , то в этом случае сумма слагаемых в решении дает выражение , которое стремится к 0 лишь при a_i<0.

Поэтому для устойчивости линейной автоматической системы необходимо и достаточно, чтобы вещественные части всех корней характеристического уравнения были отрицательны.

Факт устойчивости или неустойчивости зависит  только от структуры системы и значений ее параметров, но не зависит от внешних воздействий.

5.2 Связь переходного процесса с расположением корней на комплексной плоскости

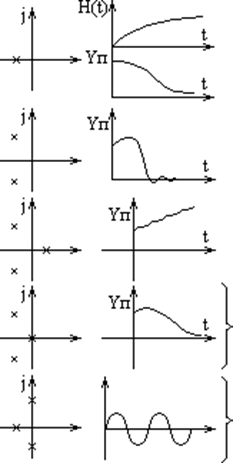
Точки, отображающие расположение корней характеристического уравнения на комплексной плоскости, называются полюсами системы. По их расположению можно судить об устойчивости системы.

Единственный полюс в левой полуплоскости - система устойчива.

Пара комплексных полюсов в левой полуплоскости -система устойчива.

Один из полюсов в правой полуплоскости = система неустойчива.

- а периодическая граница устойчивости

 - колебательная граница устойчивости

          Чтобы система была устойчивой необходимо, но недостаточно, чтобы все коэффициенты характеристического уравнения были положительны. Если хотя бы один коэффициент £ 0 – система или неустойчива, или находится на границе устойчивости, т.е. не работоспособна.

Для систем 1-го и  2-го порядка необходимое условие является и достаточным ,для более высокого порядка недостаточно.

Например: D(p)=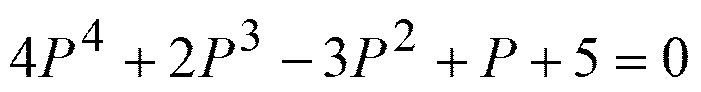- система неустойчива, так как имеется отрицательный коэффициент -3.

D(p)=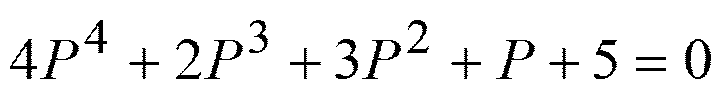                                        

 - систему нужно исследовать            

Вместо решения алгебраического уравнения и поиска корней имеются упрощенные методы исследования по критериям устойчивости.

 Критерии устойчивости

 Критерий устойчивости Рауса - Гурвица

Для того, чтобы все корни характеристического уравнения: 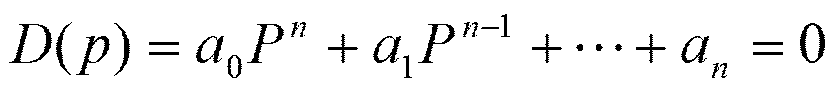 были вещественными отрицательными или комплексными с отрицательной вещественной частью ,необходимо и достаточно, чтобы при а₀>0 все определители Гурвица D_к ,получаемые из матрицы были положительными.