

Извилистое движение колесной пары.
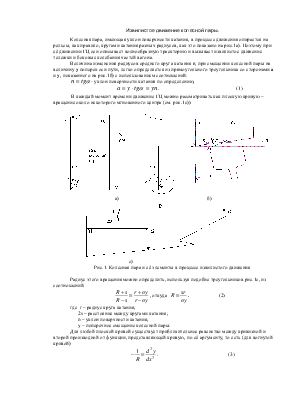
Колесная пара, имеющая уклон поверхности катания, в процессе движения опирается на рельсы, как правило, кругами катания разных радиусов, как это показано на рис.1а). Поэтому при её движении ГЦ оси описывает волнообразную траекторию и вызывает извилистое движение тележки и боковые колебания частей вагона.
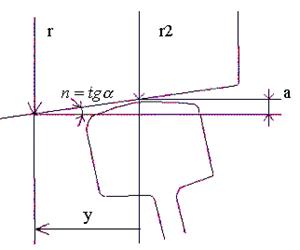
Величина изменения радиусов среднего круга катания r, при смещении колесной пары на величину y поперек оси пути, легко определяется из прямоугольного треугольника со сторонами а и y, показанного на рис.1б) с использованием соотношений:
![]() -
уклон поверхности катания по определению;
-
уклон поверхности катания по определению;
![]() .
(1)
.
(1)
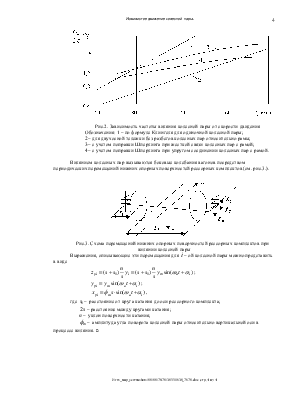
В каждый момент времени движение ГЦ можно рассматривать как плоскую кривую – вращение около некоторого мгновенного центра (см. рис.1с)).
 |
с)
Рис.1. Колесная пара и её элементы в процессе извилистого движения
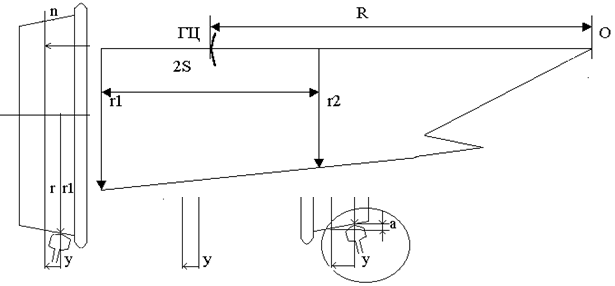
Радиус этого вращения можно определить, используя подобие треугольников рис.1с, из соотношений:
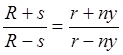 , откуда
, откуда 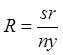 ,
(2)
,
(2)
где r – радиус круга катания;
2s – расстояние между кругами катания;
n – уклон поверхности катания;
y – поперечное смещение колесной пары.
Для любой плоской кривой существует приблизительное равенство между кривизной и второй производной от функции, представляющей кривую, по её аргументу, то есть (для вогнутой кривой)
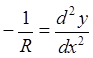 . (3)
. (3)
Подставив в это соотношение найденное ранее выражение, определяющее R, получим математическое описание (уравнение движения) ГЦ колесной пары:
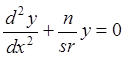 (4)
(4)
Решение этого уравнения и будет представлять закон смещений ГЦ колесной пары при её движении по рельсовому пути.
Это решение будем искать в виде гармонической функции
![]() (5)
(5)
Подставим (5) в (4), приведем подобные:
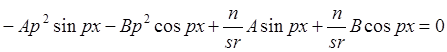 .
.
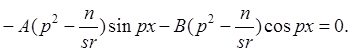
Потребуем, чтобы правая и левая части полученного выражения были равны для любого значения x. Чтобы это требование выполнялось достаточно выражение в скобках приравнять к нулю
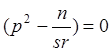
Таким образом, выражение (5) является решением уравнения (4) при условии
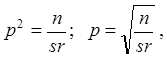 (6)
(6)
A и B – произвольные постоянные.
Для их определения зададимся
конкретными начальными условиями. Пусть в момент начала отсчета x (x=0) ![]() .
.
Тогда, используя первое
начальное условие и выражение (5) получим: ![]() .
.
Выпишем первую производную от выражение (5)
![]()
Использовав его, и второе
начальное условие, найдем: 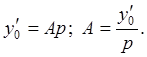
Итак, движение ГЦ колесной пары определяется выражением
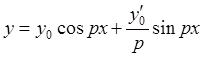 , (7)
, (7)
где 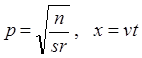 .
.
Для дальнейшего использования функции, определяющие полученное решение удобно сложить. Это можно сделать, если представить их амплитуды в виде
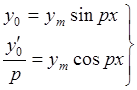 , откуда, возведя в квадрат левые и правые части и сложив их, получим
, откуда, возведя в квадрат левые и правые части и сложив их, получим 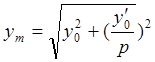 . Далее, разделив левые и правые части
друг на друга, найдем
. Далее, разделив левые и правые части
друг на друга, найдем
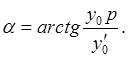
Тогда решение (7) примет вид:
![]() или
или
![]() (8)
(8)
Чтобы представить этот процесс
во времени, примем скорость движения в малый промежуток времени постоянной – ![]() и выпишем соотношения между
производными по независимым координатам
и выпишем соотношения между
производными по независимым координатам ![]() с
учетом, что
с
учетом, что ![]()
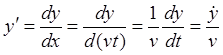 и
и 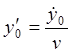 .
.
С учетом представленных соотношений решение (8) примет вид:
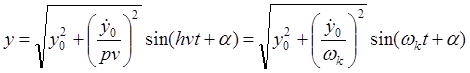 ,
,
где 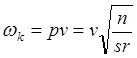 –
частота извилистого движения одиночной колесной пары по Клингелю.
–
частота извилистого движения одиночной колесной пары по Клингелю.
Определим период и длину волны этого движения
Период ![]() –
время полного колебания ГЦ можно найти из соотношения
–
время полного колебания ГЦ можно найти из соотношения
![]() откуда
откуда 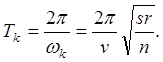
Длина волы ![]() – путь, пройденный колесной парой за
время одного периода
– путь, пройденный колесной парой за
время одного периода
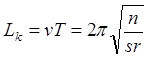
Итак получены выражения, определяющие частоту, период и длину волны извилистого движения одиночной колесной пары, которые носят название формул Клингеля.
При объединении колесных пар в раме двухосной тележки при условии, что не будет поперечных разбегов и что оси колесных пар перпендикулярны оси тележки, длину волны извилистого движения совершаемого шкворнем тележки будет определять выражение
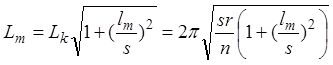 ,
,
где ![]() –
половина базы тележки.
–
половина базы тележки.
Эксперименты показывают, что формулы Клингеля дают хорошую сходимость с опытными данными лишь для скоростей движения до 60 – 65 км/ч. При более высоких скоростях длина волны начинает расти, а частота остается почти постоянной. Это объясняется ростом гироскопических и инерционных сил с ростом скорости движения.
Для высоких скоростей частоту
извилистого движения колесной пары определяют с учетом поправки Шперлинга по
формуле: ![]() .
.
Значение коэффициента ![]() определяется:
определяется:
а) для колесных пар упруго
соединенных с рамой тележки 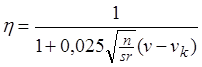 ;
;
![]()
б)
для колесных пар жестко связанных с рамой в поперечном оси пути
направлении 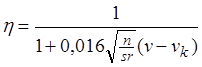 .
.
ЦНИИ МПС на основе результатов испытаний поезда "Аврора»" предложена формула
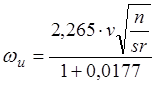 .
.
Сопоставление результатов в графической форме представлено на следующем графике
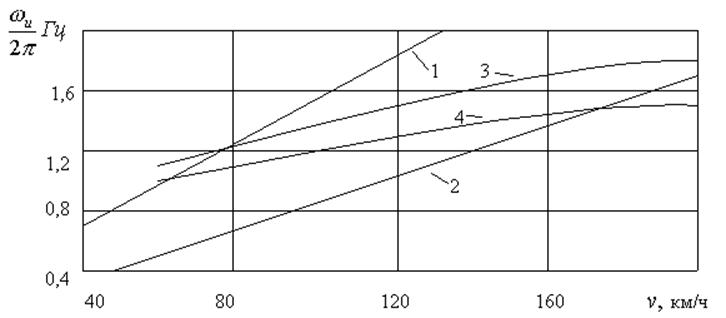
Рис.2. Зависимость частоты виляния колесной пары от скорости двидения Обозначения: 1 – по формуле Клингеля для одиночной колесной пары;
2 – для двухосной тележки без разбегов колесных пар относительно рамы;
3 – с учетом поправки Шперлинга при жесткой связи колесных пар с рамой;
4 – с учетом поправки Шперлинга при упругом соединении колесных пар с рамой.
Вилянием колесных пар вызываются боковые колебания вагонов посредством периодических перемещений нижних опорных поверхностей рессорных комплектов (см. рис.3.).
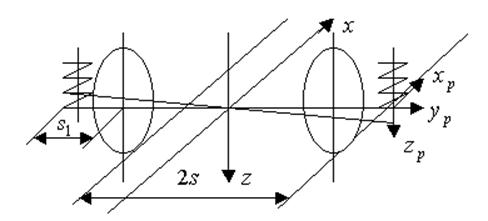
Рис.3. Схема перемещений нижних опорных поверхностей рессорных комплектов при вилянии колесной пары
Выражения, описывающие эти
перемещения для ![]() – ой колесной пары можно
представить в виде
– ой колесной пары можно
представить в виде
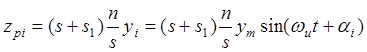 ;
;
![]() ;
;
![]() ,
,
где ![]() –
расстояние от круга катания до оси рессорного комплекта;
–
расстояние от круга катания до оси рессорного комплекта;
![]() – расстояние между кругами катания;
– расстояние между кругами катания;
![]() –
уклон поверхности катания;
–
уклон поверхности катания;
![]() –
амплитуда угла поворота колесной пары относительно вертикальной оси в процессе
виляния. ם
–
амплитуда угла поворота колесной пары относительно вертикальной оси в процессе
виляния. ם
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.