Лабораторная работа № 3.
КОМПЕНСАЦИЯ ИНЕРЦИОННОСТИ САУ
Цель работы: научиться строить различные виды обратной связи; освоить методов повышение качества САУ с помощью программы МВТУ.
1. Охват жесткой обратной связью (ОС).
Жесткой называется такая ОС, когда весь выходной сигнал возвращается на вход и вычитается из входного сигнала.
В качестве исследуемого объекта в работе используется инерционное звено с передаточной функцией вида:
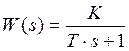
Обратная связь вводится с помощью сумматора Операции-->Сумматор . К одному из входов сумматора подключается генератор ступенчатого воздействия.
К другому входу подключается сигнал отрицательной ОС. Чтобы в сумматоре происходило вычитание нужно в свойствах сумматора Весовые множители для каждого и входов написать равными 1 -1. К выходу сумматора подключается инерционное звено Динамические-->W=K/[TS+1]
На выход инерционного звена подключить осциллограф.
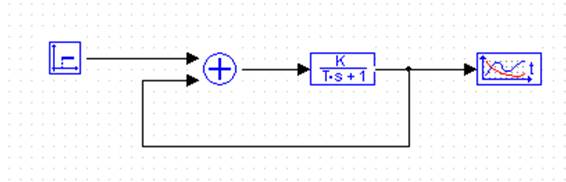
Рисунок 1 – Схема охвата жесткой обратной связью
Кроме того, для сравнения, к другому входу осциллографа подключите такое же инерционное звено, но без обратной связи.
Такое же звено дополнительно подключать во всех дальнейших экспериментах.
Содержание эксперимента.
1.1. Определить без ОС и с включенной ОС коэффициент
передачи звена ![]() и
время
и
время ![]() , в течение
которого выходной сигнал нарастает до 0,95 от установившегося значения.
, в течение
которого выходной сигнал нарастает до 0,95 от установившегося значения.
Результаты оформить в виде таблицы:
|
без ОС |
с ОС |
|
|
|
||
|
|
Сделать вывод о влиянии жесткой ОС на свойства инерционного объекта.
1.2. Для восстановления коэффициента
передачи, уменьшившегося после включения ОС, последовательно со звеном,
охваченным ОС изменить коэффициент передачи. Определить ![]() и
и ![]() в этом случае.
в этом случае.
2. Охват инерционной ОС.
Лучшие параметры САУ можно получить, если жесткую ОС заменить инерционной ОС. Для этого используется схема п. 1.2., но имеющуюся обратную связь необходимо разомкнуть и в разрыв включить такой же блок передаточных функций для создания инерционной ОС. Параметры этого блока должны быть такими, чтобы он моделировал такое же инерционное звено, как и исследуемое звено в п.1.1. Тогда его передаточная функция будет иметь вид:
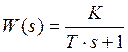 .
.
Содержание эксперимента.
2.1. Определить величину ![]() и перерегулирование
и перерегулирование 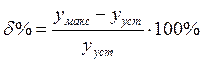 .
.
Чем объяснить существенное повышение быстродействия и появление перерегулирования при использовании инерционной ОС по сравнению с жесткой ОС?
2.2.Изменить
Т так, чтобы перерегулирование отсутствовало, а ![]() было минимально возможным.
было минимально возможным.
Результаты оформить в виде таблицы:
|
Т=1 |
Т=? |
|
|
|
||
|
|
3. Последовательное включение корректирующего звена.
Для коррекции последовательно с некорректированным
инерционным звеном с передаточной функцией 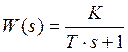 включается корректирующее звено с
передаточной функцией
включается корректирующее звено с
передаточной функцией
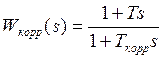 , (1)
, (1)

Тогда результирующая передаточная функция:
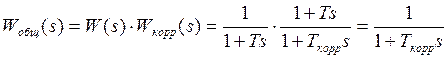
Постоянная времени корректирующего звена ![]() выбирается из условия
Tкорр<T, тогда инерционность системы уменьшается. Реализовать
корректирующее звено без потери усиления можно следующей схемой с ОС:
выбирается из условия
Tкорр<T, тогда инерционность системы уменьшается. Реализовать
корректирующее звено без потери усиления можно следующей схемой с ОС:
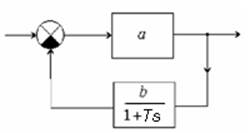
Для ее построения используется безинерционное звено с коэффициентом передачи К=а и инерционное звено. Передаточная функция такого корректирующего звена:
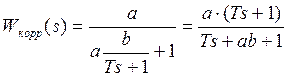 , иначе:
, иначе:
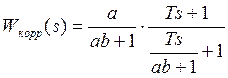 , (2)
, (2)
Сравнивая (а) и (b) можно определить, что для полной
коррекции необходимо выполнение условия 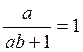 , или а=
, или а=![]() , тогда
, тогда 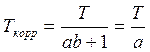 . Поэтому необходимый коэффициент
усиления безынерционного звена:
. Поэтому необходимый коэффициент
усиления безынерционного звена:
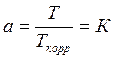 , (3)
, (3)
Задавая величину ![]() можно определить коэффициент усиления
инерционного блока:
можно определить коэффициент усиления
инерционного блока:
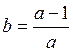 , (4)
, (4)
Содержание эксперимента.
3.1. Собрать схему, содержащую инерционное звено, использовавшееся в предыдущих экспериментах.
Сначала определить ![]() и
и ![]() без корректирующего звена.
без корректирующего звена.
3.2. Затем соединить последовательно с ним корректирующее звено. Уменьшить инерционность системы в 2 раза путем соответствующего выбора коэффициентов a и b. Определить быстродействие системы и ее общий коэффициент передачи. Результаты работы оформить в виде таблицы:
|
Без коррекции |
с коррекцией |
|
|
|
||
|
|
||
|
|
||
|
|
3.3. Поменять местами корректируемое и корректирующее звено и повторить измерения п.3.2. На другой канал осциллографа подать сигнал после корректирующего звена. Объяснить как физически происходит коррекция в обоих вариантах включения корректирующего звена.
4 Применение PID регулятора
На рис.1 показана коррекция САУ (инерционного звена) с помощью последовательно c ним включенного PID регулятора. Он представляет собой параллельно соединенные пропорциональное звено (Р), интегратор (I) и дифференциатор (D) с регулируемыми коэффициентами передачи. PID регулятор может быть включен как после корректируемого звена, так и перед ним.
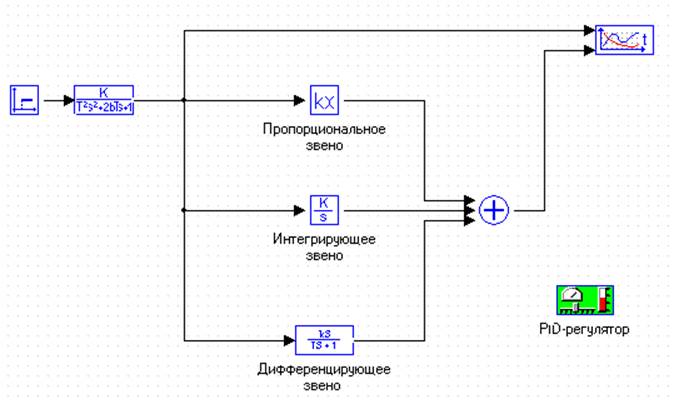
Рисунок 2 – Коррекция САУ с помощью последовательно включенного PID регулятора
4.1. Открыть схему ЛР3_Схема_7_PID-регулятор.mrj в папке Лабораторные работы
4.2 Соберите схему следящей САР с обратной связью. Установите коэффициенты PID регулятора Kп=1, Ки=0, Кд=0. При таких значениях коэффициентов PID регулятор не оказывает влияния на свойства системы.
4.3 Исследуйте влияние изменения каждого коэффициента в отдельности на погрешность и взаимодействие. Затем, изменяя все три коэффициента, найдите их оптимальные значения, при которых возможно большее быстродействие и меньшая погрешность.
5.Уменьшение статической погрешности следящей системы.
На рис.32 представлена система стабилизации выходного сигнала САУ.
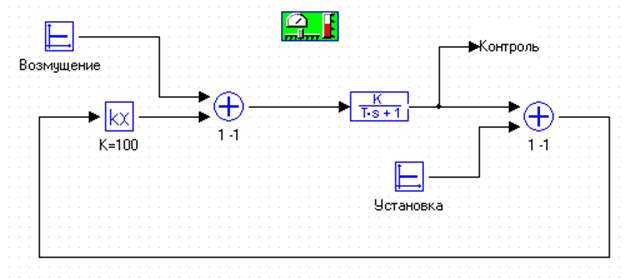
Рисунок 3 - Система стабилизации выходного сигнала САУ
На выходе объекта управления (точка Контроль) должно быть получено значение y ,совпадающее с величиной y0 сигнала установка. Если эти значения не равны ,то возникает сигнал отрицательной обратной связи, уменьшающий разность y-y0.Однако разность не может уменьшится до нуля, так как тогда сигнал обратной связи обратился бы в нуль .Поэтому сигнал y “следит” за сигналом y0 с некоторой погрешностью. Обратная связь уменьшает также и влияние возмущения.
5.1. Построить
график зависимости ошибки ![]() выходного параметра
выходного параметра ![]() от величины возмущения
от величины возмущения ![]() для глубины ОС 10 и
100 и трех значений установки
для глубины ОС 10 и
100 и трех значений установки ![]() в диапазоне 0-40. Построить
соответствующие графики
в диапазоне 0-40. Построить
соответствующие графики ![]() при ОС=const для трех значений
при ОС=const для трех значений ![]() .
.
5.2. Объясните механизм стабилизации.
6. Контрольные вопросы
1) Как влияет изменение коэффициентов PID регулятора на свойства системы?
2) Почему в следящей системе с обратной связью, не содержащей интегратора, нельзя получить погрешность равную нулю?
3) Почему включение интегратора позволяет свести погрешность практически к нулю
7.Содержание отчета
7.1 Модели и результаты измерений п.п. 1.1,1.2,2.1,2.2,3.1,3.2,3.3,4.1,4.3,5.1,5.2.
7.2. Ответы на все поставленные вопросы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.