Развитие современной науки и техники неразрывно связано с созданием новых машин, повышающих производительность и облегчающих труд людей. Машина была и остается основой технического прогресса. В основе машиностроения лежит наука ТММ, т.е. наука об общих методах исследования свойств механизмов и машин, проектирование их схем независимо от конкретного назначения машины. ТММ изучает структуру, кинематику и динамику механизмов в связи с их анализом и синтезом.
В ходе данного курсового проекта предстоит:
· Выполнить структурный анализ, определить степень подвижности механизма, класс и порядок заданного механизма;
· Выполнить кинематический анализ, построить планы скоростей и ускорений для заданного положения механизма, определить величины и направления угловых скоростей и угловых ускорений звеньев;
· Выполнить кинетостатический расчёт, определить силы инерции и моменты сил инерции звеньев, построить план нагрузки механизма. Затем при помощи рычага Жуковского определена уравновешивающая сила.
· Построить картину зубчатого зацепления
Основной целью курсовой работы является овладевание методикой исследования плоских механизмов и построения внешнего зубчатого зацепления.
Задание
Схема №17 (механизм привода к насосу), вариант №4
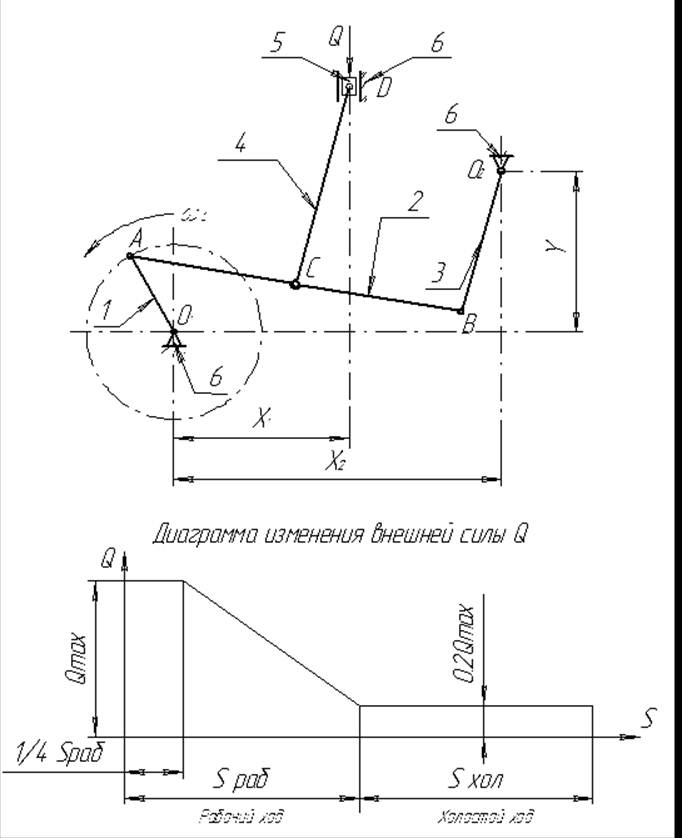
Исходные данные
|
X1, мм |
X2, мм |
Y, мм |
O1A, мм |
AB, мм |
O2B, мм |
CD, мм |
AB/BC |
|
420 |
800 |
500 |
150 |
850 |
425 |
425 |
2:1 |
Определим степень подвижности данного механизма по формуле Чебышева:
![]()
где n - число звеньев, из которых состоит механизм
P5 - число низших кинематических пар
P4 - число высших кинематических пар
Исследуемый механизм состоит из 6 звеньев (n=6):
· кривошипы 1 и 3;
· звенья 2 и 4;
· ползун 5;
· неподвижная стойка 6;
Число низших кинематических пар равно:
![]()
![]() P5 = 6 - 1 = 7
P5 = 6 - 1 = 7
1 - 2
2 - 3
6 - 3
2 - 4
4 - 5
5 - 6
Высшие кинематические пары в состав исследуемого механизма не входят, поэтому P4 = 0
Таким образом, степень подвижности данного механизма будет равна:
![]() это
значит, что исследуемая система действительно является механизмом и необходимо
одного параметра для того, чтобы определить его положение.
это
значит, что исследуемая система действительно является механизмом и необходимо
одного параметра для того, чтобы определить его положение.
Воспользуемся классификацией, предложенной Л. В. Ассуром. Для этого сначала составим структурную схему механизма, заменив звено АСВ на базисное звено 2, а ползун на поводок 5, закреплённый одним концом на стойке 6.
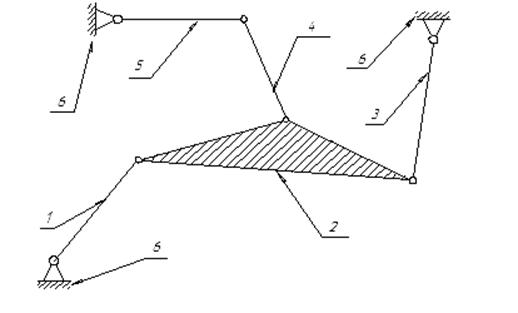
В структурной схеме нет замкнутых контуров, нет соединённых между собой базисных звеньев, но есть стойка и поводок. Значит, исследуемый механизм следует отнести к механизмам первого класса.
Разобьём механизм на группы Аcсура:
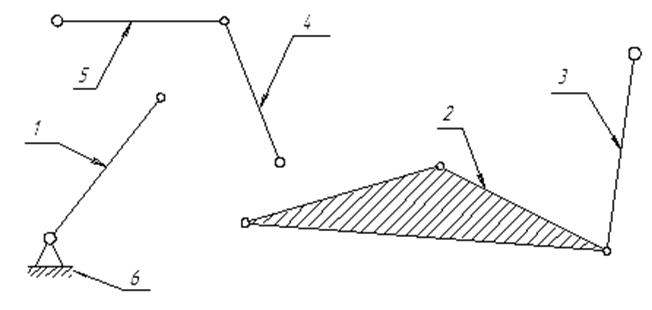
Видно, что максимальное число поводков в отдельно взятой группе - два (группа 4 - 5 - 6). Это значит, что порядок механизма равен двум.
Следовательно, исследуемый механизм является механизмом I класса 2 порядка. Такие механизмы легко исследуются методом планов.
Для определения начала цикла, крайних положений ползуна, построения траекторий движения точек механизма пользуются графическим методом исследования. Вычерчивают механизм в 12-ти положениях за один полный оборот пальца кривошипа, нумеруя точки каждого положения. Затем определяют начало цикла работы механизма, принимают это положение за нулевое и производят перенумерацию положений.
После этого, по заданию, необходимо начертить механизм в заданном положении, которое затем исследовать при помощи планов скоростей и ускорений.
Определим скорость точки А:
![]() , но т.к.
, но т.к. ![]() , то
, то
![]() ,
,
где ![]() - угловая скорость
- угловая скорость
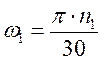 ,
,
где ![]() об/мин – частота вращения
об/мин – частота вращения
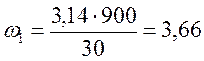
![]() ;
;
![]()
![]() ;
;
Определяем вычислительный масштаб скорости. Для этого выбираем произвольно отрезок PVА , на который изображаем скорость в точке А.
PVА =220 (мм)
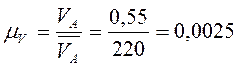
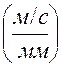 ;
;
Определяем скорость в точке В. Так как шатун АВ совершает сложное плоскопараллельное движение, то скорость любой точки шатуна можно представить состоящую из двух скоростей:
1. Скорость любой точки поступательного движения (VА , VO2)
2. Скорость другой точки во вращательном движение относительно точки (VВА , VBO2)
Составим векторные уравнения:
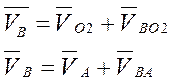
Вектор скорости точки С находим из отношения:
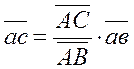
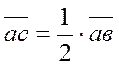 (мм);
(мм);
Определяем ускорение в точке А:
![]()
так как ![]() , то
, то ![]()
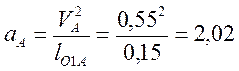
![]() ;
;
Находим вычислительный масштаб ускорения:
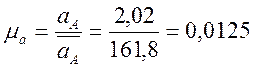
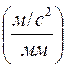 ;
;
Уравнения для определения
ускорения в точке ![]() будут следующими:
будут следующими:
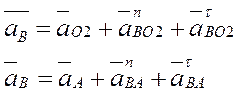
Ускорение точки С найдём из
пропорции: 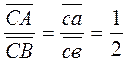
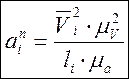 Определяем нормальные
ускорения остальных звеньев:
Определяем нормальные
ускорения остальных звеньев:
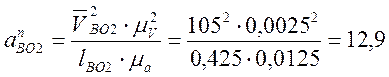
![]() ;
;
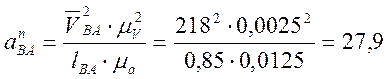
![]() ;
;
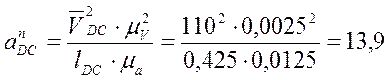
![]() ;
;
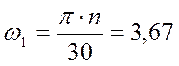 (с-1);
(с-1);
Пользуясь планом скоростей, определяем остальные угловые ускорения:
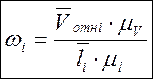
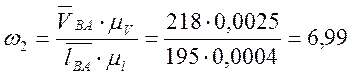 (с-1);
(с-1);
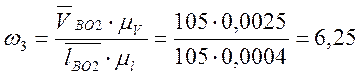 (с-1);
(с-1);
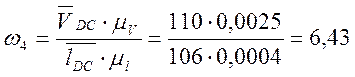 (с-1);
(с-1);
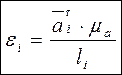
![]()
 (с-2);
(с-2);
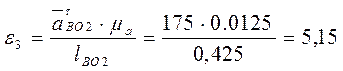 (с-2);
(с-2);
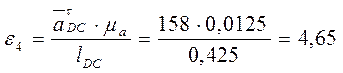 (с-2);
(с-2);
![]()
![]() Силы инерции
приложены в центре масс и направлены противоположно ускорениям соответствующих
центров масс:
Силы инерции
приложены в центре масс и направлены противоположно ускорениям соответствующих
центров масс:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
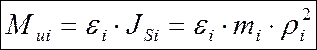
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
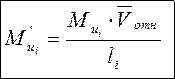
![]()
![]()
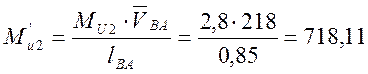
![]()
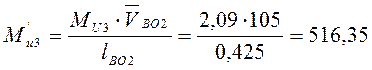
![]()
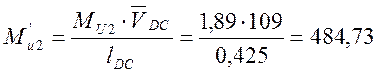
![]()
![]()
![]()
Силы тяжести приложены в центрах масс звеньев:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
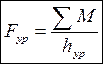 3.4 Определение
уравновешивающей силы
3.4 Определение
уравновешивающей силыУравновешивающая сила определяется по формуле:
где ∑M - суммарный момент, равный сумме моментов всех сил, приложенных к механизму относительно полюса Pv;
hур - плечо силы Fур.
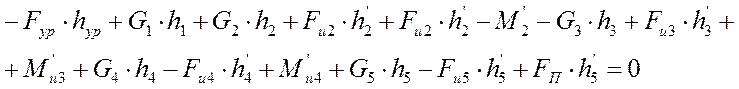
Полезная нагрузка
определяется по чертежу на диаграмме изменения внешней силы:![]() Н, плечи всех сил измеряются на
чертеже.
Н, плечи всех сил измеряются на
чертеже.
Подставляя полученные данные в выражение для суммы моментов и выразив из него Fур, получаем:
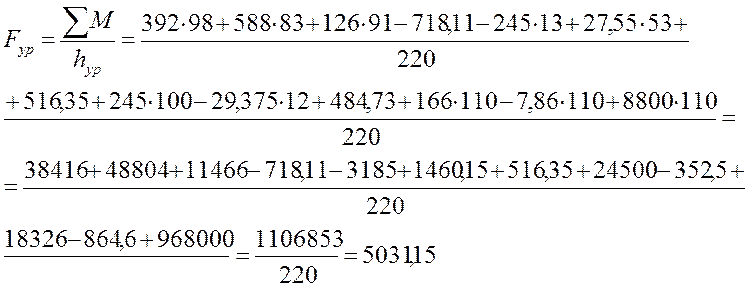
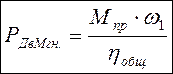
![]()
![]()
![]() Н∙м
Н∙м
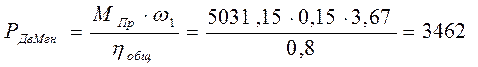
![]()
Коэффициент скорости:
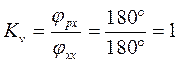
Исходные данные:
Модуль m=5
Число зубьев шестерниZ1=18
Передаточное числоU=2,5
Расчёты:
Число зубьев колеса: ![]()
Диаметры окружностей:
Для шестерни:
делительной: ![]() мм
мм
выступов (головок): ![]() мм
мм
впадин (ножек): ![]() мм
мм
основной: ![]() мм
мм
Для колеса:
делительной: ![]() мм
мм
выступов (головок): ![]() мм
мм
впадин (ножек): ![]() мм
мм
основной: ![]() мм
мм
Радиусы окружностей шестерни:
делительной: 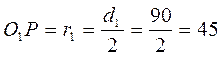 мм
мм
основной: ![]() мм
мм
выступов (головок): ![]() мм
мм
впадин (ножек): 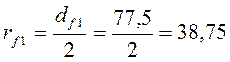 мм
мм
Радиусы окружностей колеса:
делительной: 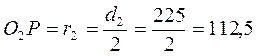 мм
мм
основной: ![]() мм
мм
выступов (головок): ![]() мм
мм
впадин (ножек): 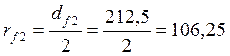 мм
мм
Межосевое расстояние: 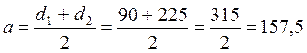 мм
мм
Шаг зубьев по делительной
окружности: ![]() мм
мм
Толщина зуба по
делительной окружности: 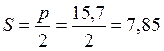 мм
мм
Радиальный зазор: ![]() мм,
мм,
где ![]() - коэффициент радиального зазора.
- коэффициент радиального зазора.
Шаг зацепления: ![]() мм
мм
Высота головки зуба: ![]() мм
мм
Высота ножки зуба: ![]() мм
мм
Высота зуба: ![]() мм
мм
В результате исследования механизма на провёртываемость установлено, что он работает стабильно, без заклинивания. Коэффициент скорости равен 1. Определена мгновенная мощность для заданного положения, она равна 3462 Вт.
Построено эвольвентное внешнее зубчатое зацепление.
Работу выполнил:_________ ___ __________ 2005 г.
1. И. И. Артоболевский “Теория механизмов и машин”, изд. “Наука”, Москва, 1975.
2. В. И. Княжкин “Эвольвентные цилиндрические зубчатые передачи внешнего зацепления”, тип. ЛИИЖТ, Ленинград, 1973.
3. А. С. Кореняко “Курсовое проектирование по теории механизмов и машин”, изд. “Машиностроение”, Москва, 1964.
4. Конспект лекций по дисциплине “Теория механизмов и машин”
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.