Ряд является знакочередующимся, поэтому по следствию
из признака Лейбница 
. Очевидно, что уже третий
член ряда 
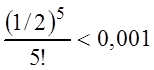, поэтому n = 2 и с точностью
до 0,001:
.
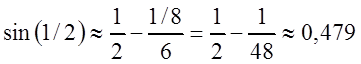Для вычисления, например, 
,
надо 
перевести в радианы.
б) Для вычисления 
сначала
представим
, так, чтобы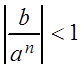 
и
запишем:
.
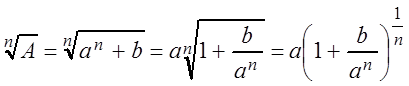Далее, применяем биномиальный ряд, в котором полагаем
, 
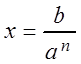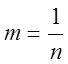. Для нашего случая: 
.
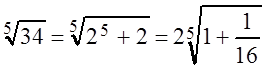Положим в ряде 
, 
,
тогда
,
.
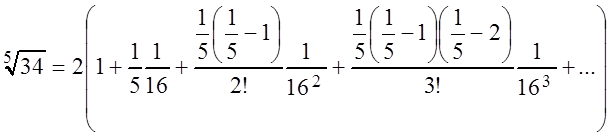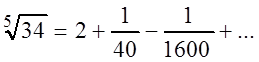Поскольку уже третий член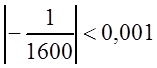 
,
то, следовательно, 
и с точностью до 0,001: 
.
Так как степенные ряды можно почленно интегрировать по любому отрезку, лежащему внутри их интервала сходимости, то с помощью разложения подынтегральной функции в степенной ряд можно находить приближенное значение определенного интеграла.
Пример 1.
Вычислить приближенно с точностью до 0,001 определенный интеграл: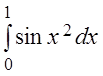 
.
Решение.
Подынтегральная функция 
такова, что ее
первообразная не выражается в элементарных функциях. Применим ряд для 
, получим:
,
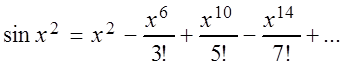для любого x: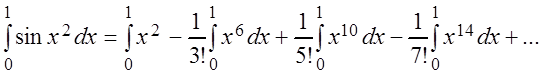 
,
,
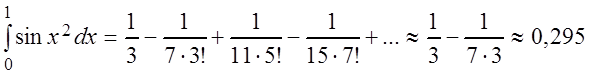так как уже третий член полученного знакочередующегося ряда меньше 0,001.
Пример 2. Вычислить приближенно с точностью до 0,01 интеграл:
.
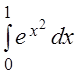Решение.
Первообразная функции 
также не выражается через
элементарные функции:
,
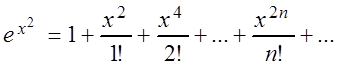для любого x (здесь использован ряд Маклорена
для функции 
)
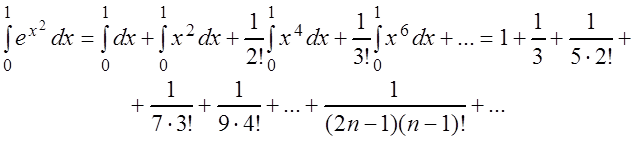
Для оценки остатка ряда воспользоваться следствием из признака Лейбница не удается, так как полученный ряд не знакочередующийся. Поступим следующим образом:
.
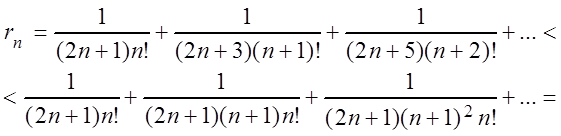
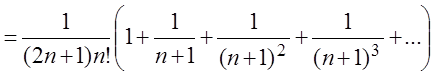В скобках получили сумму бесконечно убывающей
геометрической прогрессии, которая равна 1: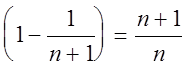 
.
Поэтому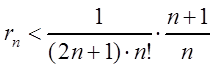 
.
Вычисляя правую часть этого неравенства при различных n
(n = 1, 2, 3, 4, ...), видим, что при n = 4: 
. Следовательно, для вычисления
данного интеграла с точностью до 0,01 достаточно взять S4, т.е.
.
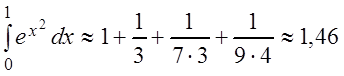Иногда точно проинтегрировать дифференциальное уравнение не удается. В этом случае бывает удобно искать решение в виде степенного ряда.
Пример 1.
Дано дифференциальное уравнение: 
. Найти частное решение,
удовлетворяющее начальному условию y(1) = 1, в виде ряда Тейлора (взяв
первые 5 его членов).
Решение. Пусть решением является
Начальное условие y(1) = 1 дает первый член
этого ряда. Подставим x = 1 и y = 1 в данное уравнение 
, получим: 
.
Продифференцируем исходное уравнение:
,
, 
,
,
, 
и т.д. Подставим найденные значения в ряд, получим:
Пример 2. Найти 6 первых членов разложения в
степенной ряд решения дифференциального уравнения 
,
удовлетворяющего начальным условиям y(0) = –2, 
.
Решение. Поскольку x0 = 0, то решение отыскиваем в виде ряда Маклорена
.
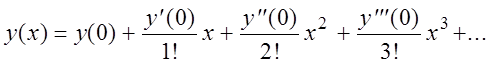Дано, что y(0)
= -2, . Подставив в данное уравнение 
начальные условия, получим: 
Дифференцируя исходное уравнение,
последовательно находим:
, 
,
,
, 
,
.
Подставив найденные значения в ряд, получаем:
.
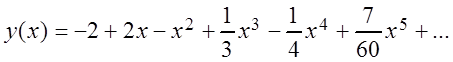Пример 1. Разложить в ряд Фурье функцию f(x), имеющую период 2p и заданную на промежутке (-p, p] следующим образом:
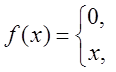
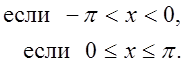
Решение.
Функция f(x) имеет точки разрыва 
,
(рис. 4.2).
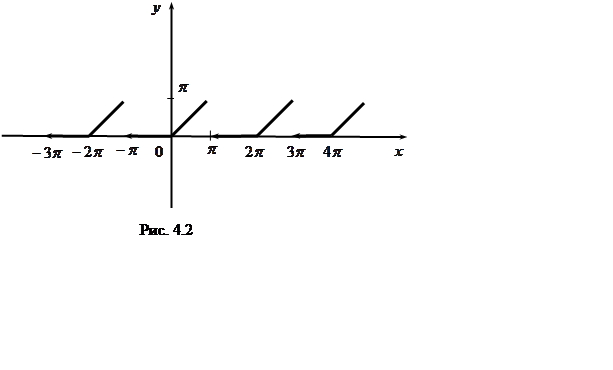
Так как f(x)
кусочно-монотонна и имеет на отрезке [-p, p] лишь одну
точку разрыва 1-го рода (
, 
), то во всех точках x
непрерывности f(x) разлагается в ряд Фурье. Находим коэффициенты
ряда:
.
,
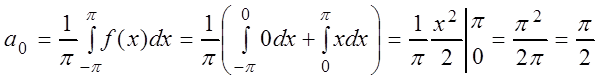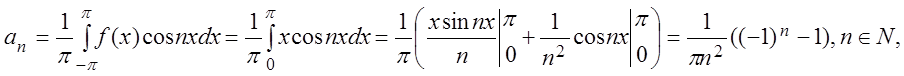
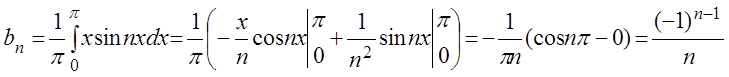n Î N. Подставляя найденные коэффициенты в ряд, получаем:
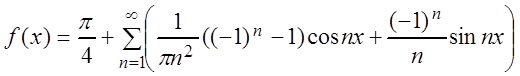
для любого 
,
k Î Z. В точках 
сумма найденного ряда:
.
Пример 2.
Разложить в ряд Фурье периодическую функцию f(x) с периодом
2l = 4, заданную на промежутке (–2, 2] равенством: f(x) =
.
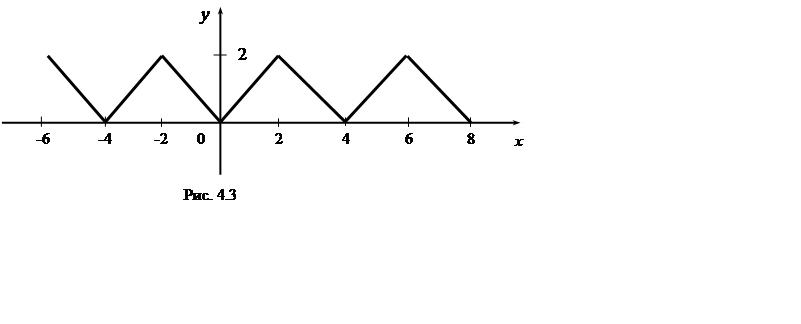
Решение. Функция f(x) определена и непрерывна на
всей числовой оси и кусочно-монотонна на отрезке [–2, 2] ( рис. 4.3).
Вычислим коэффициенты ряда Фурье:
,
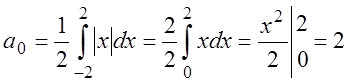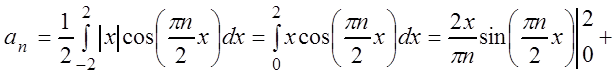
Окончательно:
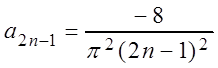, и 
.
При вычислении a0 и an было использовано свойство четной функции j(x):
.
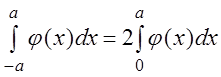При вычислении bn используем свойство нечетной функции:
,
так как подынтегральная функция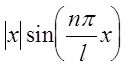 
нечетная. Ряд Фурье для данной функции
сходится к этой функции для любого x, так как f(x)
непрерывная для любого x. Итак,
.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.