Определим вид частного решения неоднородного
уравнения. Правая часть ![]() . Частное
решение: yч.н=
. Частное
решение: yч.н=![]() , так как k= 2 –
корень кратности s = 2 характеристического уравнения. Найдем производные
от этой функции:
, так как k= 2 –
корень кратности s = 2 характеристического уравнения. Найдем производные
от этой функции:
![]() ,
, ![]() .
.
Подставим значения y, y¢ и y² в данное уравнение, получим:
![]()
или ![]() ,
откуда
,
откуда ![]() .
.
Таким образом, частное решение неоднородного уравнения:
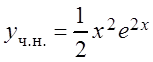 .
.
Общее решение определяется формулой:
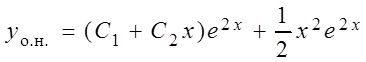 .
.
Найдем С1 и С2, используя начальные условия:
![]() , y(0) =
C1 = 1,
, y(0) =
C1 = 1, ![]() ,
,
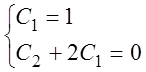
![]()
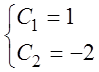 ,
,
получаем частное решение неоднородного уравнения:
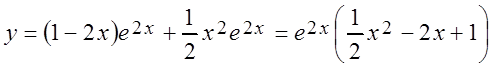 .
.
Пример
2. Найти общее решение
уравнения ![]() .
.
Решение.
Корни характеристического уравнения: ![]() будут мнимые
будут мнимые ![]() . Общее решение однородного уравнения
. Общее решение однородного уравнения
![]() будет:
будет:
![]() .
.
Определим частное решение неоднородного уравнения ![]() :
:
![]() ,
, ![]()
![]()
![]() ,
,
так
как число ![]() является корнем характеристического
уравнения, здесь s = 1, то частное решение имеет вид yч.н. =
является корнем характеристического
уравнения, здесь s = 1, то частное решение имеет вид yч.н. = ![]() . Найдем y¢, y²:
. Найдем y¢, y²:
![]() ,
,
![]() .
.
Из тождества, которое получается после подстановки y, y¢, y² в исходное уравнение, получим:
![]() .
.
Приравниваем коэффициенты при cosx и sinx,
получим: A = 0, B = 2, следовательно, yч.н =![]() . Тогда общее
решение уравнения
. Тогда общее
решение уравнения ![]() будет:
будет:
yо.н. = yо.o. + yч.н. = ![]() .
.
Пример 1. Дана система линейных дифференциальных уравнений с постоянными коэффициентами:
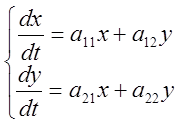 .
(4.3)
.
(4.3)
Требуется:
1) найти общее решение системы с помощью характеристического уравнения;
2) записать в матричной форме данную систему и ее решение.
Решение
a) Запишем характеристическое уравнение системы (4.3)
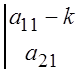
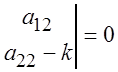 .
.
б) Найдем корни характеристического уравнения k1 и k2.
в) Запишем систему уравнений:
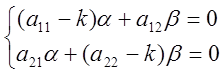 ,
,
подставим в эту систему значения k1 и k2 и определим числа
![]() ,
,
являющиеся решением этой системы.
г) Получим частные решения системы:
![]() .
.
д) Зная частные решения, составим решение данной системы (4.3):
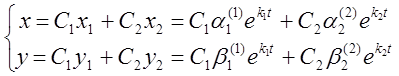 .
.
Запишем матрицу системы линейных уравнений:
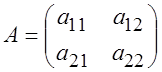 ,
,
матрицу из неизвестных:
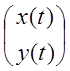 .
.
Тогда данную систему можно записать в матричной форме:
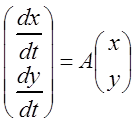 ,
,
а, следовательно, общее решение системы имеет вид
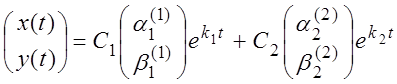 .
.
Пример 2. Найти общее решение системы:
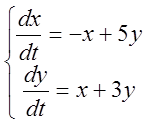 .
.
Решение
1) Характеристическое уравнение системы имеет вид:
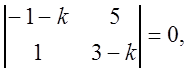
![]()
![]()
![]() .
.
Находим числа a и b, составляем систему:
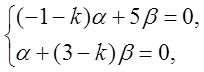
подставим k1 = 2, получим:
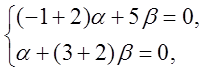
откуда
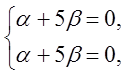
![]() .
.
Возьмем ![]() , тогда
, тогда ![]() . Подставим k2 = 4, получим:
. Подставим k2 = 4, получим:
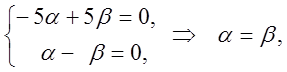
тогда
![]() .
.
Частные решения системы имеют вид:
![]() .
.
Отсюда получим общее решение системы:

2) Запишем данную систему в матричной форме:
 – матрица
системы,
– матрица
системы, 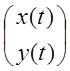 – матрица из неизвестных функций.
– матрица из неизвестных функций.
Тогда данную систему запишем в виде:
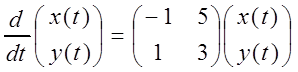 ,
,
и
ее решение в матричной форме имеет вид: 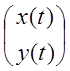 =
=
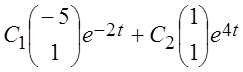 .
.
Пример 1.
Исследовать ряд: 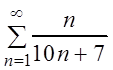 на сходимость.
на сходимость.
Решение. 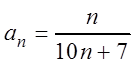 ,
, 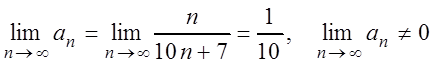 .
.
По необходимому признаку заключаем, что данный ряд расходится.
Пример 2. Исследовать на сходимость ряд:
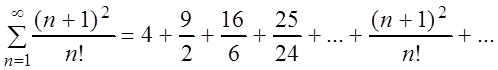
Решение. Применим к этому ряду признак Даламбера:
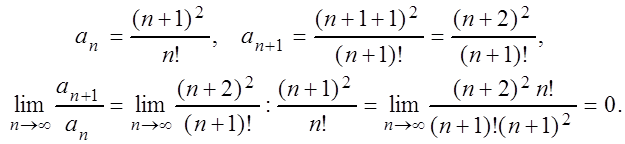
Так как d = 0 < 1, то ряд сходится по признаку Даламбера.
Пример 3. Исследовать на сходимость ряд:
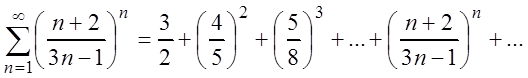
Решение. Применим к ряду признак Коши:
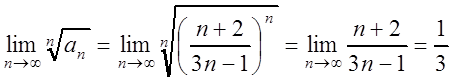 .
.
Так как k = ![]() <
1, то ряд сходится.
<
1, то ряд сходится.
Пример 4. Исследовать на сходимость ряды:
а) 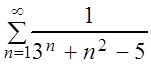 , б)
, б) 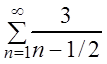 ,
в)
,
в) 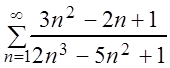 .
.
Решение
а) Сравним члены ряда 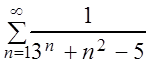 с
членами ряда
с
членами ряда 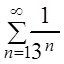 , который сходится:
, который сходится: 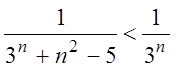 для всех n. Поэтому
данный ряд сходится.
для всех n. Поэтому
данный ряд сходится.
б) Сравним
члены ряда 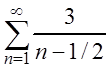 с членами гармонического ряда:
с членами гармонического ряда:  . Так
как гармонический ряд расходится, то данный ряд расходится по признаку сравнения.
. Так
как гармонический ряд расходится, то данный ряд расходится по признаку сравнения.
в) Сравним ряд 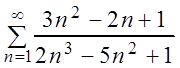 с
гармоническим рядом
с
гармоническим рядом 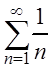 и применим предельный
признак сравнения:
и применим предельный
признак сравнения:
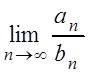 =
=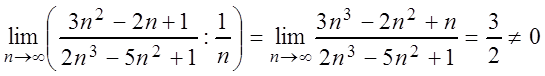 .
.
Следовательно, данный ряд расходится, так как гармонический ряд расходится.
Пример 1. Исследовать на сходимость ряды:
а) 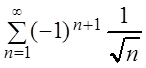 , б)
, б) 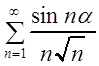 .
.
Решение
а) Применим признак Лейбница:
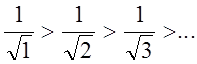 и
и  .
.
По признаку Лейбница ряд 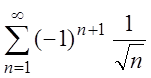 сходится,
причем условно, так как ряд
сходится,
причем условно, так как ряд 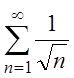 расходится.
расходится.
б) При a ¹ pk, k Î Z, данный ряд является знакопеременным, но не обязательно знакочередующимся. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
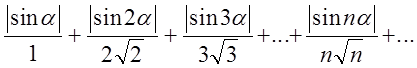
исследуем ряд на сходимость. Сравним его с рядом:
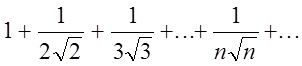
Ряд сходится
как обобщенный гармонический ряд с 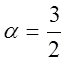 . Кроме того,
. Кроме того, 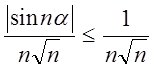 . По сравнительному признаку ряд
сходится, а поэтому сходится данный ряд, причем абсолютно.
. По сравнительному признаку ряд
сходится, а поэтому сходится данный ряд, причем абсолютно.
Пример 2. Исследовать на сходимость следующие ряды:
а) 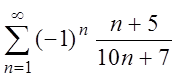 , б)
, б)  ,
в)
,
в)  .
.
Решение
а) Так как 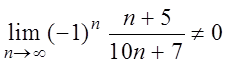 , то данный ряд
расходится по необходимому признаку сходимости рядов.
, то данный ряд
расходится по необходимому признаку сходимости рядов.
б) Для ряда 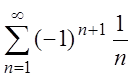 выполняются
условия теоремы Лейбница (проверьте!), значит, этот ряд сходится. Чтобы
выяснить, сходится ряд абсолютно или условно, надо исследовать на сходимость
ряд, составленный из абсолютных величин, т.е. ряд
выполняются
условия теоремы Лейбница (проверьте!), значит, этот ряд сходится. Чтобы
выяснить, сходится ряд абсолютно или условно, надо исследовать на сходимость
ряд, составленный из абсолютных величин, т.е. ряд 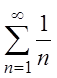 .
Но это гармонический ряд, мы знаем, что он расходящийся. Значит, данный ряд сходится
условно.
.
Но это гармонический ряд, мы знаем, что он расходящийся. Значит, данный ряд сходится
условно.
в) Так как ряд 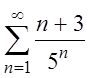 сходится
(докажите!), то ряд
сходится
(докажите!), то ряд 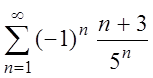 тоже сходится, причем
абсолютно.
тоже сходится, причем
абсолютно.
Пример 3. Найти сумму ряда: 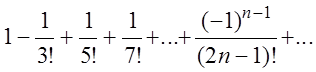 приближенно с
точностью до 0,001.
приближенно с
точностью до 0,001.
Решение.
Этот ряд удовлетворяет условиям признака Лейбница, поэтому сходится и ![]() , т.е.
, т.е. 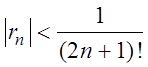 .
Выясним, при каком n выполняется условие
.
Выясним, при каком n выполняется условие ![]() .
Так как
.
Так как 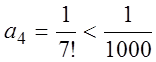 , то
, то 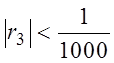 .
Возьмем S » S3,
.
Возьмем S » S3,
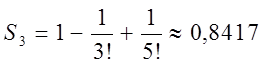 .
.
Итак, S » 0,842 причем ошибка не превышает 0,001.
Пример 1. Hайти область сходимости степенного ряда:  .
.
Решение. Для данного ряда
![]() ,
, 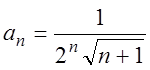 ,
,
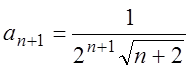 ,
, 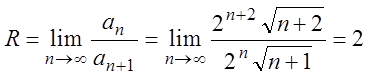 .
.
Следовательно, радиус сходимости данного ряда R = 2, интервал сходимости (4, 5). При x = 1 данный ряд превращается в числовой ряд:
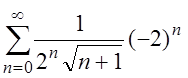 , т.е. ряд
, т.е. ряд 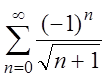 ,
,
который сходится по признаку Лейбница как знакочередующийся, но сходится условно. Следовательно, x = 1 принадлежит области сходимости данного ряда.
При x = 5
получаем числовой ряд: 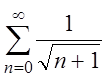 , который
расходится (докажите это). Поэтому областью сходимости ряда:
, который
расходится (докажите это). Поэтому областью сходимости ряда:
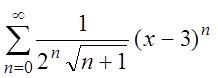
является промежуток [1, 5).
Пример 2. Доказать, что областью
сходимости ряда: 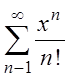 является вся числовая ось.
является вся числовая ось.
Решение.  , следовательно, областью сходимости
является интервал (-¥, +¥).
, следовательно, областью сходимости
является интервал (-¥, +¥).
Пример 3. Разложить в ряд Маклорена f(x) = ex.
Решение. Найдем производные функции f(x) = ex и вычислим их при x0 = 0:
![]() ,
,
![]() ,...,
,..., ![]() ,
...
,
...
Значит, ![]() ,
, ![]() , ... ,
, ... , ![]() ,
... .
,
... .
Остаточный член:
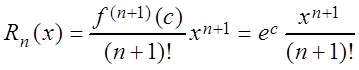 ,
,
где число c лежит между числами 0 и x. Отсюда следует, что
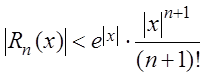 .
.
Покажем, что для любого x: ![]() при n ® ¥.
при n ® ¥.
Ряд 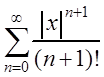 сходится при
любом x (проверьте это), поэтому
сходится при
любом x (проверьте это), поэтому 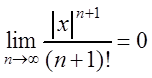 .
Значит, при любом фиксированном x:
.
Значит, при любом фиксированном x: ![]() .
Следовательно, для любого x
.
Следовательно, для любого x
 .
.
Пример 4. Разложить в ряд Маклорена функции:
а) ![]() , б)
, б) ![]() , в)
, в) ![]() .
.
Решение
а) По определению косинуса гиперболического 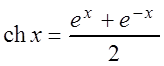 . Используем разложение функции
. Используем разложение функции ![]() в ряд:
в ряд:
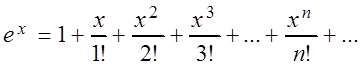 .
.
Заменяя в этом равенстве x на (–x) получим:

для любого x. Складывая почленно эти ряды, имеем:
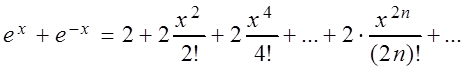
После деления обеих частей на 2 получаем равенство:
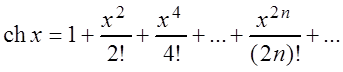 ,
,
справедливое для любого x.
б) Известно, что 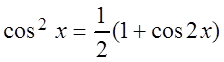 .
Разложение в степенной ряд функции cos2x легко получить из ряда
Маклорена для cosx, заменив x на 2x:
.
Разложение в степенной ряд функции cos2x легко получить из ряда
Маклорена для cosx, заменив x на 2x:

Отсюда
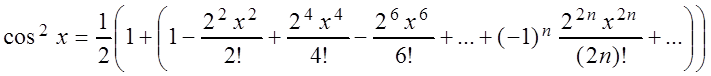 ,
,
окончательно:
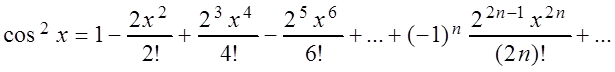
Это равенство справедливо для любого x.
в) Так как 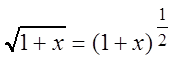 , то по
биномиальному ряду имеем:
, то по
биномиальному ряду имеем:
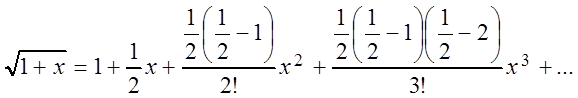
После упрощения получим:
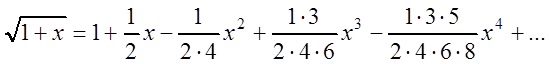
Равенство справедливо при ![]() .
.
Пример.
Вычислить с точностью до 0,001 а) 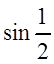 , б)
, б) ![]() .
.
Решение
а) Разложим функцию sinx в ряд Маклорена при ![]() (радиана), это можно сделать, так как
равенство справедливо для любого x:
(радиана), это можно сделать, так как
равенство справедливо для любого x:
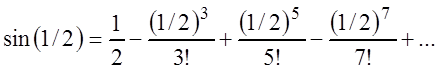
Надо найти n, при котором ![]() и ошибка не больше, чем e = 0,001.
и ошибка не больше, чем e = 0,001.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.