Определение электродных потенциалов металлов. Изменение величины электродного потенциала цинка в зависимости о концентрации раствора соли цинка

Санкт-Петербургский Государственный Университет Информационных Технологий, Механики и Оптики

кафедра

физики и техники оптической связи

ЛАБОРАТОРНАЯ РАБОТА №5

ОПРЕДЕЛЕНИЕ ЭЛЕКТРОДНЫХ ПОТЕНЦИАЛОВ МЕТАЛЛОВ

Студент        

Группа          1222

Преподаватель  

Коллоквиум ______________

Цель работы

Определить электродные потенциалы Cu, Pb, Zn, Fe, Ni. Изучить изменение величины электродного потенциала цинка в зависимости о  концентрации раствора соли цинка.

Теоретическая часть

Любой металл обладает растворимостью  в электролите, пусть даже ничтожной. Если металлическую пластинку погрузить, к примеру, в воду, то ионы металла в результате действия на них полярных молекул воды могут отрываться от поверхности и переходить в прилегающий к ней слой воды; так что нейтральный до того атом превращается в положительно заряженный ион:

Ме ^o® Ме ⁿ⁺ + n ē

Процесс носит динамический характер, так что в электролите у поверхности металла создается определенное перераспределение концентраций ионов растворителя и металла и молекул растворителя.

Итак, взаимодействие металла с водой или раствором, содержащим ионы этого металла, приводит к образованию у поверхности двойного электрического слоя и появлению разности потенциалов между металлом и раствором. Эта разность потенциалов включает в себя падение потенциала в слое адсорбированных на поверхности ионов (j_а) и падение потенциала в растворе (в диффузионном слое (j_д):

j = j_а + j_д

Переход ионов из металла в раствор – процесс обратимый и изотермический, здесь система совершает максимальную полезную работу А, характеризуемую изобарно-изотермическим потенциалом Гиббса DG°_р:

A_эл = -DG = -n×F×j

где n - заряд иона; j - разность потенциалов между металлом и раствором, F - число Фарадея.

Равновесие имеет динамический характер: часть ионов приповерхностного слоя диффундирует в электролит, другие ионы из раствора замещают их. В результате равновесная концентрация ионов металла у поверхности электрода С₀ оказывается иной, чем средняя концентрация ионов в растворе С.

Изотермическая работа по перемещению 1 моля ионов между приповерхностным слоем и объемом раствора определяется как:

А = R×T×ln(С₀/С)

Из условия равенства этих работ следует:

DG° =  -n×F×j = R×T×ln(С₀/С)

Отсюда может быть найден потенциал электрода:

R×T

j = ^______ ×ln (С/С₀)

n×F

Концентрацию С₀ определить экспериментально невозможно, поэтому потенциал изолированного электрода, погруженного в раствор электролита, рассчитать не представляется возможным. Однако можно определить разность потенциалов (ЭДС = DЕ = j₂ – j₁) между одинаковыми электродами, погруженными в раствор собственного иона, но с различной концентрацией, так называемый  концентрационный элемент:

R×T                           R×T

j₂ – j₁ = ^_____  [ln(С₂/С₀) – ln(С₁/С₀)] = ^______ ln(С₂/С₁)           

n×Fn×F

или для стандартных условий (298 К) и после замены натурального логарифма на десятичный:

j₂ – j₁ = (0,059/n) ×lg(С₂/С₁)

В электрохимии принято измерять электродные потенциалы металлов в вольтах, обозначаемые Е, по отношению к некоторому стандартному электроду сравнения, потенциал которого условно принят за нуль. По международному соглашению в качестве такого электрода сравнения применяется стандартный водородный электрод , а условной величиной, характеризующей потенциал рассматриваемого электрода, принимают ЭДС гальванического элемента, составленного из этого электрода и стандартного водородного электрода. Эту величину называют электродным потенциаломданного электрода и обозначают буквой Е^о. Таким образом, принимая концентрацию ионов металла в адсорбционном слое С₀ = 1моль/л, получаем ЭДС элемента, составленного из металлов одного вида, но с разной концентрацией ионов в растворе:

R×T

DЕ = Е-Е^о  =  ¾¾× ln(C_Meⁿ⁺)

      n×F

или:                     

         R×T

Е =  Е^о  +  ¾¾× ln(C_Meⁿ⁺)

n×F

где  C_Meⁿ⁺ – молярная концентрация ионов.

Это уравнение называется уравнением Нернста.

Уравнение является приближенным, поскольку не учитывает межионного взаимодействия в растворах электролитов. Для учета этого взаимодействия вводится активность иона, связанная с его концентрацией  следующим соотношением:

a = f×C

где f - коэффициент активности.

Уравнение для расчета электродных потенциалов также  имеет вид:

Е = Е^о  + (0,059/n) × lg(a_n-)

Порядок выполнения работы

Работа проводится в два этапа: на первом этапе измеряются стандартные электродные потенциалы металлов при их погружении в растворы соответствующих солей с концентрациями 1 моль/л; на втором этапе исследуется зависимость электродных потенциалов одного металла (цинка) при погружении его в растворы соли цинка с различными концентрациями: 0,1М; 0,5М; 1,0М и 1,5М.

1.   Получить набор электродов.

2. Перед измерениями каждый раз зачищать наждачной бумагой поверхность электрода.

3.  Последовательно подсоединять исследуемые электроды к датчику, составляя гальваническую цепь из измеряемого электрода и хлорсеребряного электрода сравнения. Оба электрода при этом должны быть погружены в раствор соответствующей соли необходимой концентрации.

4. На приборе определить ЭДС.

5. Подсчитать величину измеренной ЭДС (DЕ) в мВ. Для этого  полученное показание прибора умножить на 100.

6. После каждого измерения  хлорсеребряный электрод должен быть погружен в дистиллированную воду.

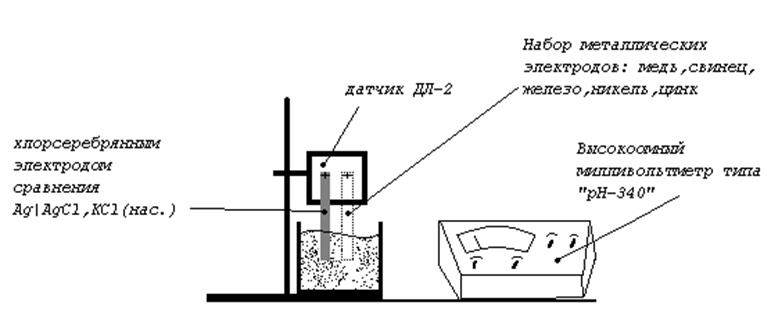
Измерения

Zn(0,1)   795 мB = 0,795 В      Zn(NO₃)₂

Zn(0,5)   807 мB = 0,807 В      Zn(NO₃)₂

Zn(1,0)   830 мB = 0,830 В      Zn(NO₃)₂

Zn(1,5)   856 мB = 0,856 В      Zn(NO₃)₂

Ni(1,0)   50 мВ  = 0,050 В      Ni(NO₃)₂

Pb(1,0)   380 мВ = 0,380 В      Pb(NO₃)₂

Fe(1,0)   463 мВ = 0,463 В      FeCl₃

Cu(1,0)   115 мВ = 0,115 В      Cu(NO₃)₂

Расчеты

E_Cu/Cu²⁺ =  DЕ + E_хс

Е_Zn/Zn²⁺ =  E_xc –½DЕ½

Е_Ni/Ni²⁺ =  E_xc –½DЕ½

Е_Fe/Fe²⁺ =  E_xc –½DЕ½

Е_Pb/Pb²⁺ =  E_xc –½DЕ½

 

E_хс = 0,202 В

DЕ – найдено нами.

E_Cu/Cu²⁺ =  0,115 + 0,202 = 0,317  В

Е_Ni/Ni²⁺  = 0,202 – 0,050 = 0,152  В

Е_Fe/Fe²⁺ =  0,202 – 0,463 = -0,261 В

Е_Pb/Pb²⁺ =  0,202 – 0,380 = -0,178 В

[E]=[B+B]=B

DG = - n×F×DЕ

DG⁰_pCu = -2*96484*0,115 = -22191,3 (дж/моль)

DG⁰_pNi = -2*96484*0,050 = -9648,4 (дж/моль)

DG⁰_pFe = -2*96484*0,463 = -89344,2 (дж/моль)

DG⁰_pPb = -2*96484*0,380 = -73327,8 (дж/моль)

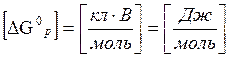
Исследуемый электрод	Схема гальванического      элемента	ЭДС,В	ЕMe/Men+ рассч.,В	E0, В	DG0p дж/моль
Cu	Cu|Cu2+||KCl,AgCl	0,115	0,317	0,340	-22191,3
Ni	Ni|Ni2+||KCl,AgCl	0,050	0,152	-0,250	-9648,4
Fe	Fe|Fe2+||KCl,AgCl	0,463	-0,261	-0,440	-89344,2
Pb	Pb|Pb2+||KCl,AgCl	0,380	-0,178	-0,130	-73327,8

Е_Zn/Zn²⁺

Экспериментальные:

(0,1 М) Е_Zn/Zn²⁺ = 0,202 – 0,795 = -0,593 В

(0,5 М) Е_Zn/Zn²⁺ = 0,202 – 0,807 = -0,605 В

(1,0 М) Е_Zn/Zn²⁺ = 0,202 – 0,830 = -0,628 В

(1,5 М) Е_Zn/Zn²⁺ = 0,202 – 0,856 = -0,654 В

Расчетные:

По формуле Нернста:

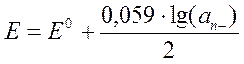
(0,1 М)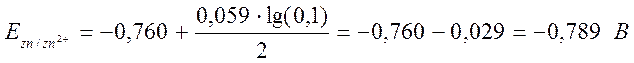  

(0,5 М)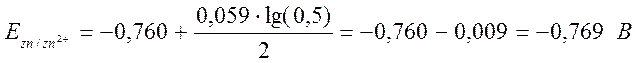  

(1,0 М)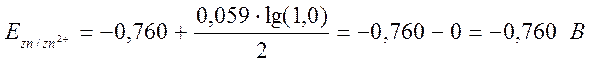  

(1,5 М)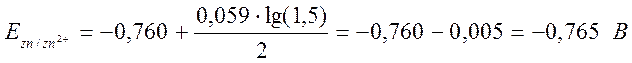  

Погрешности:

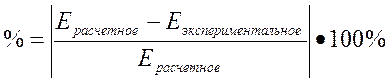
(0,1)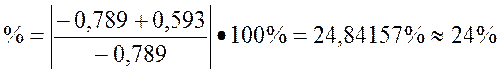

(0,5)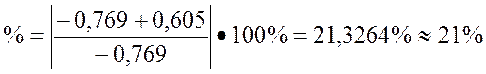

(1,0)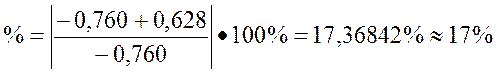

(1,5)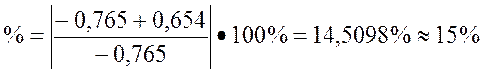

Исследуемый электрод	Схема гальванического      элемента	Концентрация электролита	ЭДС,В	Электродный потенциал Е, В		погреш- ность измере- ний
				экспер	расчетн
Zn	Zn|Zn2+||KCl,AgCl|Ag	0,1	0,795	-0,593	-0,789	24%
		0,5	0,807	-0,605	-0,769	21%
		1,0	0,830	-0,628	-0,760	17%
		1,5	0,856	-0,654	-0,765	15%

Вывод

Проведя эксперимент и сделав необходимые расчеты, мы определили электродные потенциалы меди, свинца, железа и никеля, а также изучили изменение величины электродного потенциала цинка в зависимости от  концентрации раствора соли цинка, при этом наша погрешность была от 15% до 24% вследствие некачественной зачистки электрода перед каждым измерением.

Также нашли несколько различий в теории и практике:

I

С увеличением концентрации электродный потенциал цинка увеличивался