Построение генераторов случайных чисел. Интерфейс программы. Статический анализ выходных данных моделирования

Содержание

ВВЕДЕНИЕ.. 5

§1. Выбор входных распределений. 6

Построение генераторов случайных чисел. 6

1.1 Выбор входных распределений. 6

1.2 Построение генератора случайных чисел, распределенных экспоненциально. 6

1.3 Построение генератора дискретных случайных чисел, распределенных равномерно. 8

1.4 Построение генератора случайных чисел u(0, 1), распределенных равномерно. 8

§2. ЛОГИКА ПРОГРАММЫ. 9

ИНТЕРФЕЙС. 9

2.1 Алгоритм работы программы.. 9

2.2 Интерфейс программы.. 13

§3. СТАТИСТИЧЕСКИЙ АНАЛИЗ ВЫХОДНЫХ ДАННЫХ ПРОЦЕССА МОДЕЛИРОВАНИЯ. 16

3.1 Статический анализ выходных данных моделирования. 16

3.2 Графики коэффициента использования системы, числа требований в очереди и системе для одного из прогонов. 17

3.3 Графики оценки корреляции. 19

3.4 Рекомендации по использованию результатов моделирования. 21

Заключение. 25

ВВЕДЕНИЕ

Требуется разработать программу для имитационного моделирования системы массового обслуживания с 6 устройствами. В системе интервалы времени между поступлением требований являются независимыми случайными величинами, со средним временем 60 с. Когда требование поступает, а устройство свободно, обслуживание начинается немедленно. Время обслуживания является случайной величиной, некоррелированной с интервалами поступления требований. Среднее значение времени обслуживания требований 180 с. Если при поступлении требования устройства заняты, требование становится в очередь на позицию, соответствующую приоритету заявки, сгенерированному генератором случайных дискретных чисел из интервала [1, 3].

Оценке подлежат следующие параметры:

·  коэффициент использования системы p;

·  средняя задержка в очереди d;

·  среднее время ожидания w;

·  среднее по времени число требований в очереди Q;

·  среднее по времени число требований в системе L.

Перечень вопросов, подлежащих разработке в процессе реализации проекта:

·  анализ задачи и обзор аналогов;

·  выбор входных распределений;

·  логика работы программы;

·  построение генераторов случайных чисел;

·  статический анализ выходных данных моделирования;

·  рекомендации по использованию результатов моделирования.

АНАЛИЗ ЗАДАЧИ И ОБЗОР АНАЛОГОВ

В последнее время возникла необходимость в решении различных вероятностных задач, связанных с  работой систем массового обслуживания.

Примерами    таких систем в повседневной жизни могут служить  все виды очередей: билетные кассы, турникеты в метро и многие другие ситуации, где действует принцип FIFO.

В компьютерной индустрии такие проблемы находят свое применение в различных менеджерах процессов. Решение подобной задачи просто необходимо при проектировании микрооперационных систем реального времени.

Темой данного курсового проекта является решение одной из таких задач.

Имитационная модель отображает  стохастический  процесс  смены дискретных состояний СМО в непрерывном времени в форме моделирующего алгоритма.  При его реализации на  ЭВМ  производится  накопление  статистических данных по тем атрибутам модели, характеристики которых являются предметом исследований. По окончании моделирования накопленная  статистика обрабатывается, и        результаты моделирования получаются в виде выборочных распределений исследуемых величин или их     выборочных моментов.  Таким образом, при имитационном моделировании     систем массового обслуживания речь  всегда  идет  о  статистическом имитационном моделировании. К настоящему времени имеется хорошо разработанный и широко использующийся математический аппарат имитационного моделирования систем массового обслуживания, который возник и получил практическую значимость благодаря широкой доступности вычислительных средств.

§1. Выбор входных распределений.

 Построение генераторов случайных чисел

1.1 Выбор входных распределений

В системе интервалы времени поступления и обработки требований являются случайными величинами, которые генерируются в ходе работы модели. Будем считать их распределёнными по экспоненциальному (показательному) закону. Этот выбор обусловлен тем, что данный вид распределения просто моделируется и достаточно полно характеризует поведение системы во время её функционирования. Для генерирования приоритетов заявок будем использовать генератор дискретных случайных величин, распределённых равномерно.

1.2 Построение генератора случайных чисел, распределенных экспоненциально

Экспоненциальное распределение со средним значением β (любое положительное вещественное число) является непрерывным, с плотностью распределения вероятностей

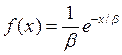
Интегральная функция распределения случайной величины X определена для любого вещественного x как . Если величина является экспоненциальной функцией X со средним значением β, то

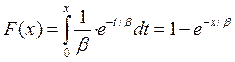
где U – величина, равномерно (непрерывно) распределенная между 0 и 1.

В модели необходимо генерировать интервалы времени поступления и обработки требований, поэтому генератор должен иметь не менее двух потоков.

Код функции ехроn, которая генерирует экспоненциально распределенную случайную величину со средним значением β = mean (переданным в функцию ехроn), представлен в листинге 1.1. Для генерирования случайных чисел с целью получения величины U используется функция lcgrand, описанная в пункте 1.4.

Листинг 1.1. Код на языке Matlab функции expon

function [result] = expon(stream, mean)