Построение генераторов случайных чисел. Интерфейс программы. Статический анализ выходных данных моделирования, страница 4

0.15787    0.069122    0.063897    0.077229    0.085389    0.067432    0.053414    0.066485    0.063605    0.058511

Математическое ожидание: 0.076295

Дисперсия: 0.00090204

Доверительный интервал (β = 0.95): [0.05768, 0.09491]

Среднее по времени число требований в системе L:

3.335      3.0079      3.0657      3.1175      3.0495      3.1009      2.9855      3.0614      3.1039      3.0143

Математическое ожидание: 3.0842

Дисперсия: 0.0096848

Доверительный интервал (β = 0.95): [3.0232, 3.1452]

Средняя задержка в стеке d:

9.4098      4.1902      3.7951      4.6068      5.1652      4.0196      3.2403      3.9534      3.7938       3.539

Математическое ожидание: 4.5713

Дисперсия: 3.1823

Доверительный интервал (β = 0.95): [3.4656, 5.677]

Среднее время ожидания w:

199.2183      182.4601      182.6569      186.0804      184.7728      185.5745      181.2906      182.5637      185.2201      182.5662

Математическое ожидание: 185.2404

Дисперсия: 26.749

Доверительный интервал (β = 0.95): [182.0348, 188.446]

3.2 Графики коэффициента использования системы, числа требований в очереди и системе для одного из прогонов

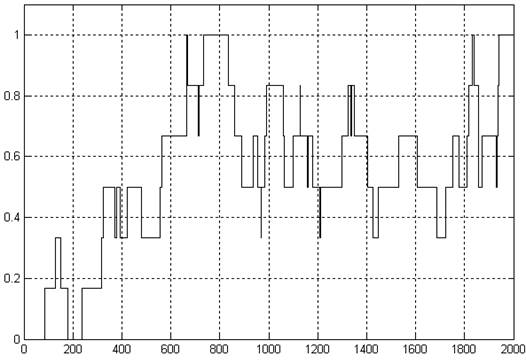
Рис. 3.1. График коэффициента использования системы

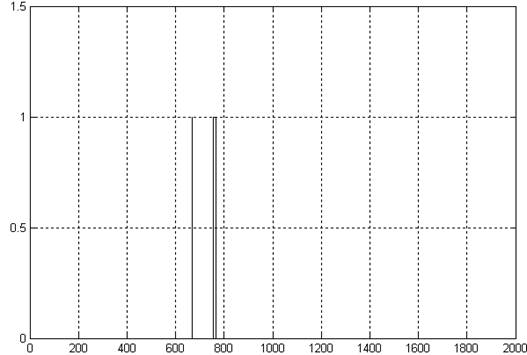
Рис. 3.2. График числа требований в очереди

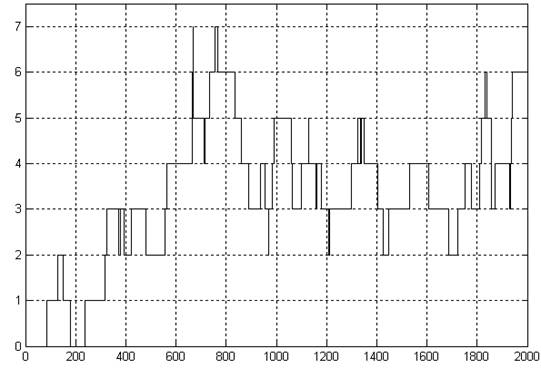
Рис. 3.3. График числа требований в системе

3.3 Графики оценки корреляции

По результатам 20 прогонов были построены графики оценки корреляции:

·  времени работы системы t (рис. 3.4)

·  коэффициента использования системы ρ (рис. 3.5)

·  средней задержки в очереди d (рис. 3.6)

·  среднего времени ожидания w (рис. 3.7)

·  среднего по времени числа требований в очереди Q (рис. 3.8)

·  среднего по времени числа требований в системе L (рис. 3.9)

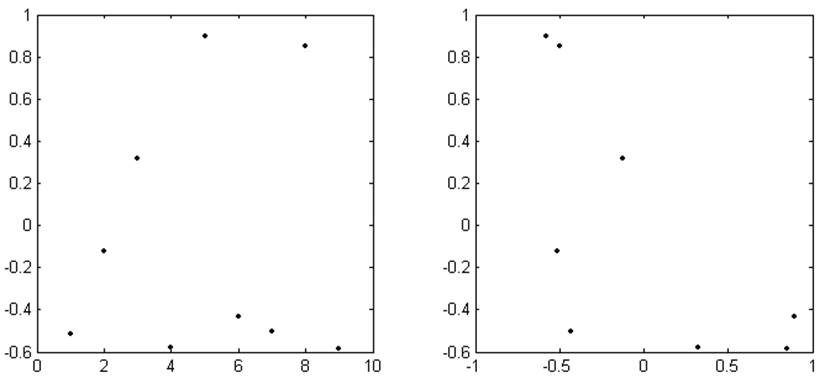
_j, ρ_j                                                                                                        ρ_{j ,} ρ_j+1

Рис. 3.4. График оценки корреляции времени работы системы t

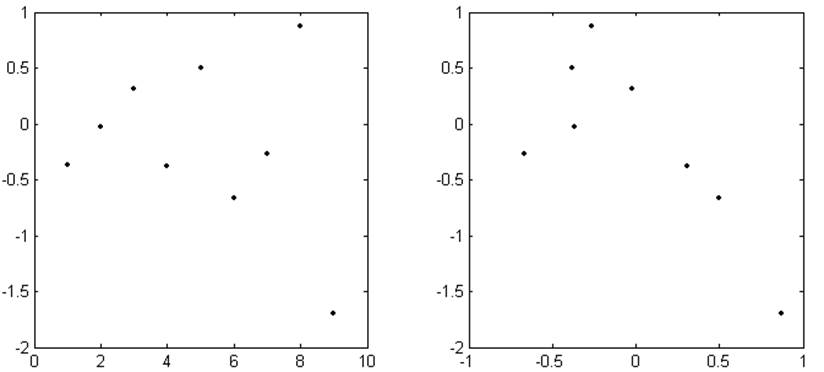
_j, ρ_j                                                                                                        ρ_{j ,} ρ_j+1

Рис. 3.5. График оценки корреляции коэффициента использования системы ρ

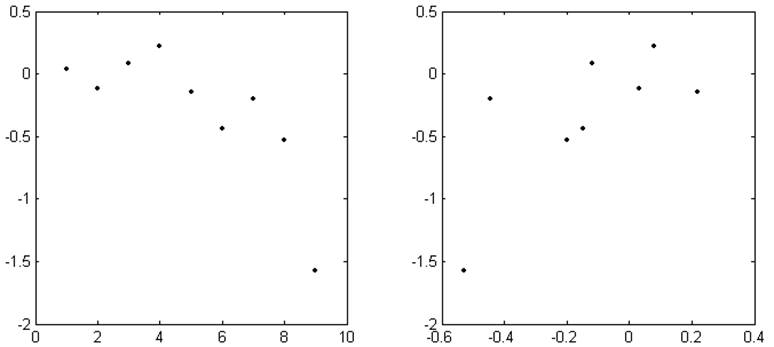
_j, ρ_j                                                                                                        ρ_{j ,} ρ_j+1

Рис. 3.6. График оценки корреляции средней задержки в очереди d

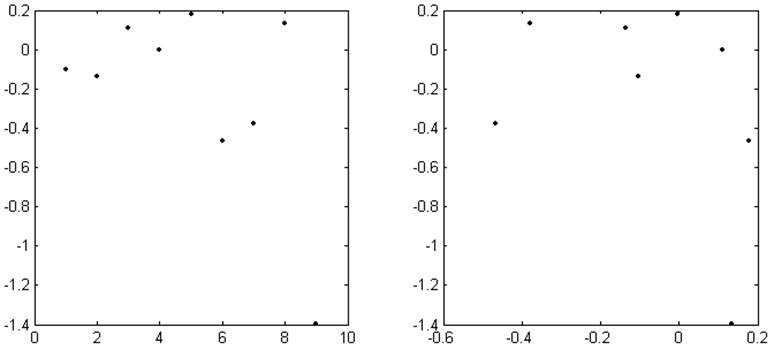
_j, ρ_j                                                                                                        ρ_{j ,} ρ_j+1

Рис. 3.7. График оценки корреляции среднего времени ожидания w

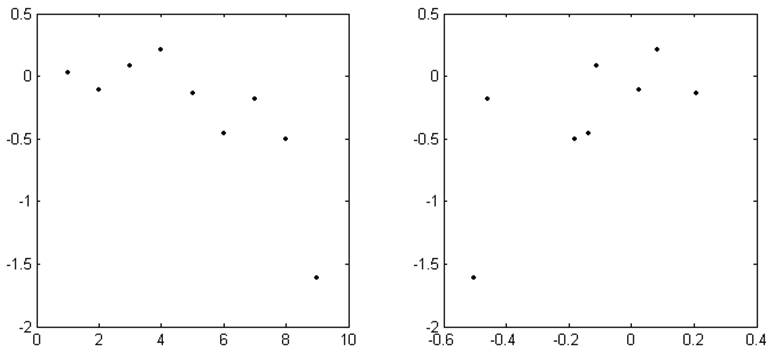
_j, ρ_j                                                                                                        ρ_{j ,} ρ_j+1

Рис. 3.8. График оценки корреляции среднего по времени числа требований в очереди Q

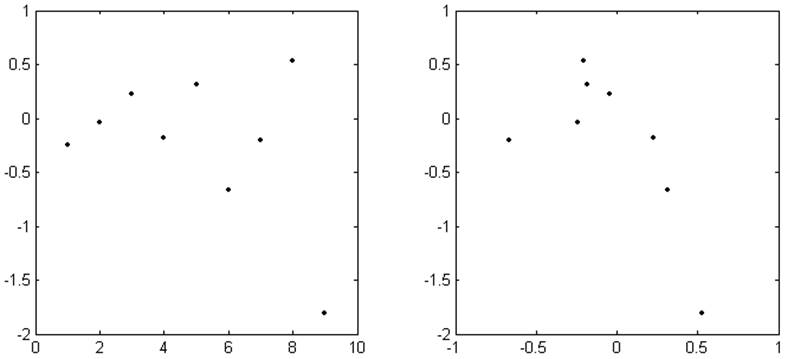
_j, ρ_j                                                                                                        ρ_{j ,} ρ_j+1

Рис. 3.9. График оценки корреляции среднего по времени числа требований в системе L

Из представленных графиков видно, что данные моделирования не имеют между собой значительной корреляции и, следовательно, пригодны для практического использования.

3.4 Рекомендации по использованию результатов моделирования

При моделировании использовались следующие условия:

·  количество устройств – 6;

·  среднее времяпоступления требований –60;

·  среднее время обработки требования – 180;

·  дисциплина обслуживания – FIFO с 3 приоритетами.

В результате моделирования получены следующие данные:

·  время работы системы t =  120111.0547;

·  коэффициент использования системы ρ = 0.821;

·  средняя задержка в очереди d = 4.5713;

·  среднее время ожидания w = 185.2404;

·  среднее по времени число требований в очереди Q = 0.076295;

·  среднее по времени число требований в системе L = 3.0842.

Коэффициент использования системы показывает, что система загружена. В этом случае система работает в предельно допустимом режиме. Данный вариант оптимален с точки зрения экономии оборудования.

1. Смоделируем работу системы с пятью устройствами (в случае отказа 1). Проведем 10 прогонов системы. Получены следующие результаты: