Математические основы моделирования социальных сетей. Примеры анализа социальных сетей

УДК 519.8

МАТЕМАТИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ СОЦИАЛЬНЫХ СЕТЕЙ

Сибирский государственный аэрокосмический университет имени академика М. Ф. Решетнева, г. Красноярск, Российская Федерация,

Аннотация. В работе приведены примеры анализа социальных сетей. Рассмотрены краткие результаты проводимых ранее экспериментов. Рассмотрены общие свойства различных видов сетей, описывающих процессы в сложных социальных системах. Перечислены основные актуальные направления моделирования и оценки социальных сетей.

Ключевые слова: социальная сеть, граф, вершины графа, транзитивность сети.

MATHEMATICAL FOUNDATIONS OF MODELING SOCIAL NETWORKS

Siberian State Aerospace University named after academician M. F. Reshetnev, Krasnoyarsk, Russian Federation,

Abstract                                                               

Examples of social networks. Considered previously held the experiments. The General properties of different types of networks describing the processes in complex social systems.

Keywords: social network, graph, vertex graph, transitivity network.

Nowadays almost everyone says the phrase “a social network”. In the second half of the 20^th century, this term was used in the West in studies of social bonds and human relations. There are some examples of social networks: 1. Contacts between separate people (personal; online; official; professional; criminal etc). 2. Network joint activities (co-authorship of scientific articles; shooting in a film; membership in an online-community etc).[1]

In 1969 American psychologists: Stanley Milgram and Jeffrey Travers put forward “six degrees of separation”. It describes the fact that every person is indirectly acquainted with any other inhabitant of the planet through a chain of acquaintances, which on average consists of five people. In different years different experiments were done, which confirmed the theory. [10]In 1967, Stanley Milgram carried out a series of experiments, which is called “Small world experiment”. Randomly selected inhabitants of Omaha (Nebraska) and Wichita (Kansas) were offered to send a letter to an addressee in Boston, using only personal contacts. Only 64 letters reached the addressees of 296 were sent. The chain length varied from 2 to 10 people. The average chain length is about 6 people. In 2003, Milgram’s experiment was done again but with the usage of email. The average chain length is about 6 people. There was a large percentage loss. In 2006 Youtube, Orkut and Flickr were explored, the average length is 4.25-5.88, the diameter of the graph is 9-27. In 2011 Facebook was explored, the average length is 4.74.

To describe models of social networks such terms are used:

·  The distance between two vertices.

·  The diameter of the graph (the number of edges connected with the given vertices).

·  The degree of a vertex.

·  The distribution of degreed of vertices.

·  The closeness centrality and the betweenness centrality.

·  The distribution of the closeness centrality.

·  The clustering coefficient.

·  The coefficient of assortativeness.[4-8]

In the random large graph every edge is present or absent with the explicit probability, the distribution of the degree of vertices is binominal or Poisson. Far from the Poisson distribution, the distribution of the degree of vertices is distorted with a slant to the right in most networks. These distributions have the long right tail part of values. A part of the vertices in the network that has a degree k,is defined as p_k. To solve the problem of determination of the distribution the data about degree is presented by formation of the cumulative distribution function: 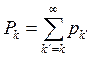, which is probability that the degree ≥ k .

D.Watts and S.Strogatz (1998) pointed that most networks have a high transitivity, which is called clustering. The presence of bonds between vertices A and B, between B and C leads to the bond between A and C. In other words, if B has two neighbours on the network A and C, they will be connected with each other based on their common connection with B. The same is in the topological terms: there is a high density of triangles ABC and the clustering can be quantified by measuring the density: