C(1) = 3× (the number of triangles on the graph) / (the number of the connected triples of vertices),
where “the connected triple” is a vertex, connected directly with an unordered pair of vertices. Actually, C measures a part of triples, which have the third edge to form a triangle. The multiplier “3” is given to account that each triangle is included in three triples, that’s why 0≤C≤1.
An alternative definition of the clustering index (Watts and Strogatz, 1998) is:
 .
.
For the vertices with the degree 0 or 1: Ci = 0 . So, the clustering index is:
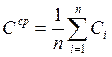 .
.
Three main directions were formed in the theory of modeling social networks:
1. Determination of statistical properties which characterize the behavior of a networked system;
2. Creating of models of networks;
3. Predicting the behavior of systems with network structure based on the measured structural properties and the local rules for the management of individual vertices.
In recent years, the study of networks focuses on the analysis of large-scale statistical properties of the network. Many of the questions, which could be asked in the study of small networks, don’t make sense in large networks. For example, “Which vertex will be most critical in a network connection if it is deleted?” – this question doesn’t make sense in large networks. On the other hand, “What percentage of vertices will be deleted to affect the network connection significantly?” – such question has real value for very large network. For networks of tens or hundreds of vertices it is not difficult to answer specific questions about the structure of the network, visually examining the image of the network. It is not possible to draw the image of the network with a very large number of vertices; perfection of statistical methods for the quantitative assessment of large networks should lead to a wider range of network analysis.
References:
1. Albert R., Jeong H., Barab´asi A. Attack and error tolerance of complex networks // Nature. 2000. Vol. 406, pp. 378–382.
2. Batygin, S., Gradoselskaja,.. Network relationships in the professional community of sociologists: the technique of content-analytical study of biographies. //Sociological journal, 2001, No. 1 . With . 156-163.
3. Bartholomew D. Stochastic models for social processes. M: FIS, 1985. 295 C.
4. Castells M. Materials for an exploratory theory of the network society. - Brit. J. of. Soc., 2000, No. 51, p.5-24.
5. Ebel H., Mielsch L., Bornholdt S. Scale-free topology of e-mail networks. // Phys. Rev. 2002. E 66.
6. Granovetter М. The Sociological Approaches to Labor Market Analysis: A Social Structural View / Granovetter Ì., Swedberg R. (eds.) The Sociology of Economic Life. Boulder, Westview Press, 1992. P. 244-245
7. Gradoselskaja Century, lecture Notes in Social networks and social theory.// Methodical materials of the national training Fund. IP SAN, PFUR. 04.2004. M. S. 293-344
8. Interfirm networks: between market and hierarchy. Internet-conference Network forms of interfirm cooperation: strategic challenges and competitive advantages of new organizations of the XXI century .04.2004.
9. Newman M.E.J. The structure and function of complex networks. // SIAM Review. 2003. Vol. 45. pp. 167–256.
10. Noda I., Suzuki S., Matsubara H., Asada M., Kitano H. Overview of RoboCup-97. // In H. Kitano (ed.), RoboCup-97: Robot Soccer World Cup I, Lecture Notes in Artificial Intelligence. 1997. Vol. 1395. Springer Verlag, pp. 20–41.
11. Milgram S. The small world problem, Psychology Today, 1967, Vol. 2, pp. 60–67.
12. Stark D., Vedres B. Social times of network spaces: sequence analysis of the formation of networks and foreign investment in Hungary, 1987-2001, Economic sociology electronic journal www.ecsoc.msses.ru. Vol. 6. No. 1. January 2005. C. 14-46.
13. Watts D.J., Strogatz S.H. Collective dynamics of ″small-world″ networks. // Nature. 1998. Vol. 393. pp. 440–442.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.