










1. Механические колебания. Виды колебаний. Характеристики колебаний.
Колебания – это движение, которое периодически повторяется. Виды колебаний:
а) свободные – это колебания, которые существуют в пространстве без поддержки внешней силы (или внутренней периодической силы).
б) вынужденные – это колебания, которые существуют благодаря внешней периодической силе.
в) автоколебания – это колебания, которые обусловлены внутренним действием системы саму на себя.
Хар-ки:
а) период – время совершения одного полного колебания.
б) частота – это число колебаний за ед времени. [ν]=1/c=c-1, T=1/ν, T=t/N, ν=N/t.
в) циклическая частота – число колебаний за 2π секунд. [ω]=Гц, ω=2π/t=2πν.
г) если колебания гармонические, то они должны удовлетворять условию периодичности колебаний x(t)=x(t+T). Уравнение гармонического колебания x=Asin(ωt+φo)=Asin((2π/T)t+φo) (либо по cos).
А – амплитуда – максимальное отклонение от положения равновесия,
φо – начальная фаза колебаний,
ωt+φo – фаза колебаний – положение системы в данный момент времени.
д) скорость совершения колебаний – первая производная от координаты по времени. x`(t)=υ(t)=Acos(ωt+φo)ω=Aωcos(ωt+φo).
υmax=Aω – макс скорость е) ускорение. a(t)=x”(t)=υ`(t)=-Asin(ωt+φo)ω2=-Aω2sin(ωt+φo), |amax|=Aω2.
ж) энергия колебаний. Энергия колебаний системы складывается из кинетической и потенциальной энергии.
2. Сложение колебаний одного направления и взаимноперпендикулярных.
Под сложением колебаний понимается нахождение закона результирующего колебания системы тел в случае, когда эта система участвует в нескольких колебательных процессах. Пусть складываются два колебания одного направления одинаковой частоты и распространяющимся по одному закону:
x1=A1sin(ωt+φ01), x2=A2sin(ωt+φ02). Применим метод векторных диаграмм:
![]() , Δφ=φ02-φ01.
, Δφ=φ02-φ01.
Частные случаи:
а) Δφ=2kπ, ![]()
б) Δφ=(2k+1)π, ![]()
Если 2 колебания распростр-ся во взаимноперпенд-х плоскостях с одинаковой частотой и по одинаковому закону: x=Asin(ωt+φ1), у=Вsin(ωt+φ2)
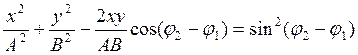
Частные случаи:
а) φ2-φ1=(2k+1)π/2, 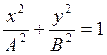 - точка движется по
эллипсу, если А=В, то по окружности.
- точка движется по
эллипсу, если А=В, то по окружности.
б) φ2-φ1=kπ, 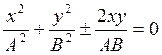
Если k – четное число, то
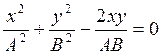 ,
, 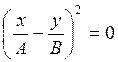 ,
,
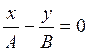 ,
, 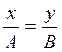 ,
,
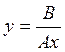 - точка движется по прямой.
- точка движется по прямой.
Если k – нечетное число,
то 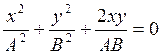 ,
, 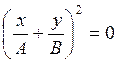 ,
,
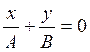 ,
, 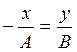 ,
,
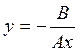 - точка движется по прямой.
- точка движется по прямой.
3. Свободные электромагнитные колебания. Колебательный контур. Уравнение колебаний заряда, напряжения и силы тока от времени.
Осуществляется в колебательном контуре, состоящем из катушки индуктивности и конденсатора, заряженного до какой-то разницы потенциалов. Сопротивление проводов принимается ≈0.
Если положение ключа в т.1, то С будет заряжаться до какой-то разности потенциалов. Если ключ переключить в положение 2, тогда С начнет разряжаться через L и в контуре будут происходить ЭМ колебания.
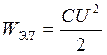 ,
, ![]() ,
, ![]()
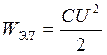 ,
, 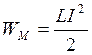 ,
, ![]()
![]() ,
, 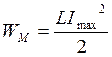 ,
, ![]()
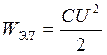 ,
, 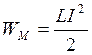 ,
, ![]()
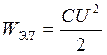 ,
, ![]() ,
, ![]()
В КК происх проебраз-е ЭМ эн-ии: эн-ии ЭП в эн-ию МП и обратно.
ΣU=Σε, 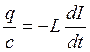 ,
, 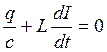 ,
, 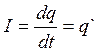 ,
, 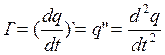 ,
, 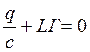 ,
, 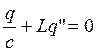 ,
, 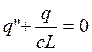 ,
, 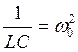 - собственная частота
колебаний в контуре,
- собственная частота
колебаний в контуре, ![]() -
диф однородное ур-е 2го порядка, q=qmaxcos(ωt+φo) – решение
этого ур-я.
-
диф однородное ур-е 2го порядка, q=qmaxcos(ωt+φo) – решение
этого ур-я.
По ур-ю можно судить, что в КК осуществляются
свободные гармонические колебания. qmax – амплитудное
значение заряда. ω=2π/Т, 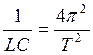 ,
, ![]() - ф-ла Томсона. U=q/C, U=Umaxcos(ωt+φo) – колебания
напряжения в контуре.
- ф-ла Томсона. U=q/C, U=Umaxcos(ωt+φo) – колебания
напряжения в контуре.
I=q`(t)=-qmaxsin(ωot+φo)ωo=-qmaxωosin(ωot+φo), |Imax|=qmaxωo.
5. Затухающие механические и электромагнитные колебания. Основные уравнения колебаний. Коэффициент затухания.
Затухающими колебаниями называются колебания,
осуществляющиеся в среде с сопротивлением. В этом случае амплитуда колебаний
убывает по ехр з-ну. А2=А1е-βТ, β – коэф
затухания среды, Т – период колебаний. Аi=А0е-βt, Ai – амплитуда в момент времени t. x=А0е-βtsin(ωt+φ0) – ур-е затухающих механических колебаний. А0 – амплитуда в
момент времени = 0, ω – установившаяся частота колебаний. ![]() , ωо – собственная
частота колебаний в системе без учета сопротивления.
, ωо – собственная
частота колебаний в системе без учета сопротивления.
Логарифмический декремент затухания показывает,
во сколько раз изменится амплитуда колебаний за 1 период. 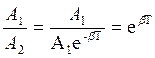 ,
, 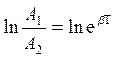 ,
,
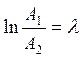 , λ=βТ. λ – лог декремент затух-я.
β=λ/Т, А2=А1е-(λ/Т)T=А1е-λ, А=А0е-(λ/Т)t
, λ=βТ. λ – лог декремент затух-я.
β=λ/Т, А2=А1е-(λ/Т)T=А1е-λ, А=А0е-(λ/Т)t
Т.о. за время t система
амплитуда уменьшается в «е» раз, а система успевает сделать N колебаний, т.е. λ показывает ту обратную величину, за которую
амплитуда уменьшается в «е» раз.
Свободные затухающие колебания осуществляются в КК с сопротивлением. ΣU=Σε, 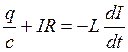 ,
, 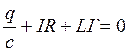 ,
, 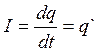 ,
, 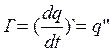 ,
, 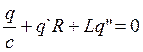 ,
, 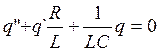 ,
, 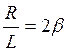 - коэф затухания, β=R/2L, β2=R2/4L2, q=qmaxе-βtcos(ωt+φo) – решение
ур-я, ω – установившаяся частота колебаний в контуре
- коэф затухания, β=R/2L, β2=R2/4L2, q=qmaxе-βtcos(ωt+φo) – решение
ур-я, ω – установившаяся частота колебаний в контуре 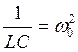 , ωо2>β2
→ колебания в контуре затухают по ехр з-ну.
, ωо2>β2
→ колебания в контуре затухают по ехр з-ну.
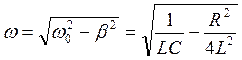 . Это ур-е
говорит о том, что колебания в контуре будут свободными гармоническими затухающими.
. Это ур-е
говорит о том, что колебания в контуре будут свободными гармоническими затухающими.
6. Основные фотометрические величины: энергетический поток, освещенность, энергетическая яркость, светимость. Переход к световым величинам.
а) световой поток – мощность светового излучения показывает, какая энергия света распространяется за ед времени. [Ф] = Люмен = Лм. 1Лм = световому потоку, излучаемому изотропным источником света с силой света в 1 Кд в пределах телесного угла 1 стерадиан.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.