Механические колебания. Виды колебаний. Характеристики колебаний. Сложение колебаний одного направления и взаимноперпендикулярных, страница 8

23. Постулаты Бора. Физический смысл постулатов. Необходимость их введения.

а) атом может длительно находиться в таких состояниях, в которых не излучает и не поглощает эн-ии. Такие состояния наз-ся стационарными.

б) орбитальный момент электронов, вращающихся на этих орбитах равен М=υ_nr_nm, υ_n – скорость ē на n-ой орбите, r_n – радиус n-ой орбиты. 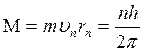, n – орбитальное число (главное квантовое число).

в) атом излучает или поглощает эн-ию, когда переходит с одного уровня на другой.

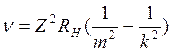- частота излучения или поглощения

Z – порядковый номер

R_H – пост Ридберга для водорода, R_H=3,28·10^-15 с^-1

m – уровень, на котором находился ē

k – уровень, на который перешел ē

24. Расчет водородоподобного атома по Бору: радиусов и скоростей электронов на орбитах. Основные выводы.

Водородоподобный атом это ядро вокруг, которого вращается 1 ē.

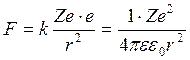  (1) - кулоновская сила (сила электростатического взаимод-я между ē и ядром)

С другой стороны это центростремит-ая сила 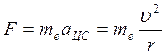 (2). (1)=(2) 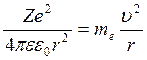,  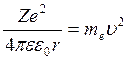(3).

Воспольз-ся 2м постулатом Бора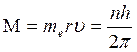

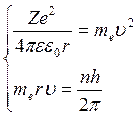
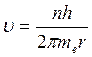 (4)

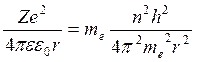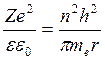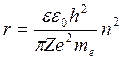, , (5)

Радиус ē в данном атоме зависит только от номера орбиты. r₁:r₂:r₃:r_n=1:4:9:n²

r_n=n² r₁. Радиус орбиты зависит от квадрата главного квантового числа.

Подставим (5) в (4) 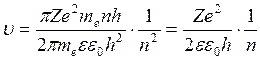. Скорость ē обратнопропорц-на главному квантовому числу υ₁:υ₂:υ₃=1:½:⅓

υ_n=υ₁/n

Теория Бора оказалась справедливой только для водородоподобного атома, поскольку она была основана на законах классической физики (з-н Кулона, 2й з-н Ньютона). Применение теории Бора для других атомов послужило тому, что теория стала расходиться с экспериментом, поэтому нужна была новая теория, описывающая атом, основывающаяся на своих собств-х з-нах. Эта теория и была предложена квантовой физикой. Теория Бора выступала в ней частным случаем.

25. Вывод кинетической, потенциальной, полной энергии электрона в водородоподобном атоме. Диаграмма переходов. Энергия ионизации.

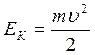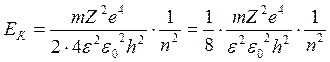, , Е_к1:Е_к2:Е_к3=1:1/4:1/9

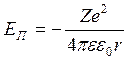- ф-ла для Еп частицы, находящейся а ЭП

Знак минус указывает, что ē связан силами притяжения к ядру.

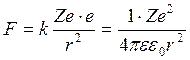 (1) - кулоновская сила (сила электростатического взаимод-я между ē и ядром)

С другой стороны это центростремит-ая сила 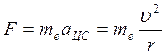 (2). (1)=(2) 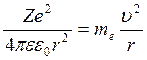, , 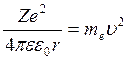, 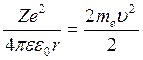|Eп|=2Ек.

Eп по модулю в 2 раза > его Ек.

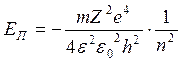, |Е_п1|:|Е_п2|:|Е_п3|=1:1/4:1/9

.

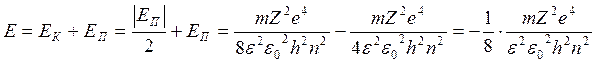Полная энергия ē всегда отрицательна и обратнопропорц-на квадрату главного квантового числа.

26. Корпускулярно-волновая двойственность частиц. Волна де Бройля. Подтверждение выводов де Бройля. Дифракция электронов, как подтверждение того, что частицы обладают волновыми свойствами.

Де Бройль предположил, что корпускулярно волновой дуализм характерен не только для света, а является универсальным свойством любых материальных объектов. Это значит, что любой частице, обладающей массой, импульсом и скоростью можно поставить в соответствие волну, т.е. эта частица хар-ся не только массой и скоростью, но и частотой и длинной волны (λ_Б). λ_Б=h/p, p – импульс частицы.

υ<<c => 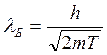, Т – кинетическая эн-ия

υ≈c => , Е₀ – эн-ия покоя частицы.

В 1927 Девиссон и Джермер поставили опыт, который подтвердил ф-лу де Бройля. ē-ны разогнанные до высокой скорости вылетают из электронной пушки, попадают на кристалл Ni так, что можно наблюдать дифракционную картину. С другой стороны часть ē-в отражается и попадает в цилиндр Фарадея, который присоединен к гальванометру. В рез-те гальванометр фиксирует ток.

а) λ₁=h/p=h/mυ, eU=mυ²/2,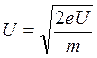

б) dsinθ=kλ₂, 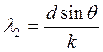, λ₁=λ₂=λ_Б

Оказалось, что длины волн, рассчитанные разными способами равны. Это значит, что ф-ла де Бройля оказалась верна. Опыт доказал правильность теории де Бройля.

Пучок ē-в проходит через очень тонкую фольгу и на экране можно наблюдать дифракционную картину, т.е. имеются участки куда попадает наибольшее число ē-в (светлые круги) и участки куда попадает их наименьшее число (темные области). Т.е. распределение инт-ти имеет вероятностный хар-р, а значит ē-ны обладают волновыми св-вами.