Механические колебания. Виды колебаний. Характеристики колебаний. Сложение колебаний одного направления и взаимноперпендикулярных, страница 3

9. Интерференция света в тонких пленках. Разность хода. Интерференция в клине. Примеры интерференции.

В тонких пленках

Лучи 1 и 1` образованы от одного источника =› они когерентны, поэтому при их наложении возникает интерференция. Пока луч 1` шел в т.В луч 1 уже прошел расстояние = АМ. Δr=r₁n₁–r₂n₂, Δr=(AD+DB)n–AMn` - оптическая разность хода лучей. Рассм ΔAOD. cosγ=AO/AD=d/AD, AD=DB=d/cosγ, sinγ=AC/AD, AC=ADsinγ=(d/cosγ)sinγ. Рассм ΔABM. Угол ABM=α, sinABM=sinα=AM/AB, AM=ABsinα. Для того чтобы найти сторону AB рассмотрим ΔADC. sinγ=AC/AD=AC/(d/cosγ)=ACcosγ/d, AB=2AC, AM=2ACsinα, AC=(d/cosγ)sinγ, AM=(2d/cosγ)sinαsinγ, sinα/sinγ=n, sinα=nsinγ, Δr=(2d/cosγ)n-(2d/cosγ)sinαsinγ=(2d/cosγ)(n-sinαsinγ)=(2d/cosγ)(n-nsinγsinγ)=(2d/cosγ)n(1-sin²γ)=(2d/cosγ)ncos²γ=2dncosγ, Δr=2dncosγ – если известен угол прелом.

Выразим разность хода ч/з угол падения sinα/sinγ=n₂/n₁, sinγ=sinα/n, 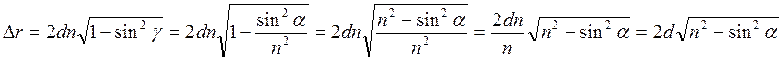- если извест угол падения.

При отраж-ии от > плотной среды луч теряет фазу на π или разность хода увелич на λ/2. Поэтому для интерференции в отраженном свете добавляется поправка +λ/2. Т.к. для проходящего света такого отражения нет, то ф-лы запишутся без поправки.

В клине

Клин – угол м/у 2мя поверхностями. Поверхности образуют клин, если угол м/у ними достаточно мал. Если угол мал, то для клина можно применять те же ф-лы, что и для плоскопараллельной пластинки. Луч1 и 1` интерферируют м/у собой, т.к. получены от одного источника, поэтому в т.А наблюдается чередование темных и светлых полос. В т.А наблюдается интерференция, при этом толщина клина в месте падения 1го луча и 2го ≈ одинаковы, то в т.А наблюдается чередование полос, отстоящих друг от друга на равном расстоянии. 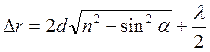- для отраженных лучей, - для проходящих.

10. Кольца Ньютона. Вывод радиусов колец в отраженном и проходящем света.

Если взять плосковыпуклую линзу и положить ее на прямую гладкую стеклянную поверхность, то просматривая ч/з эту систему поведение лучей, мы будем наблюдать кольца с общим центром. В отраженном свете центр темный, в проходящем - светлый. Это явление происходит в результате интерференции падающих или отраженных лучей. Т.к. радиус кривизны линзы достаточно большой, то можно считать распространение луча вдоль одной линии. Лучи 1` и 2` интерферируют, т.к. получены от одного источника.

Рассм ΔAOB. AO²=AB²+OB², R²=r_k²+(R-d)²=r_k²+R²-2Rd+d²=r_k²-2Rd+d², d²≈0, r_k²=2Rd, d – толщина клина в т.А, . Толщину клина найдем из того условия, что лучи 1` и 2` интерферируют в клине, тогда 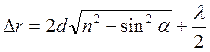- разность хода для отраженных лучей 1` и 2`, Δr=2dn+λ/2. Тогда найдем радиус светлого кольца:

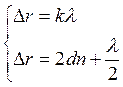
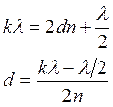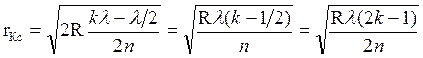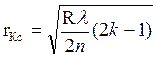     ;;- радиус светлого кольца в отраженном свете.

Найдем радиус темного кольца:

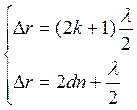
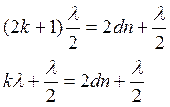
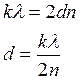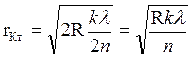        ;- радиус темного кольца в отраженном свете.

Радиусы светлых колей пропорциональны нечетным числам, а радиусы темных колец пропорциональны четным числам. В проходящем свете радиусы колец будут выглядеть наоборот, по сравнению с отраженным светом 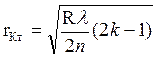, 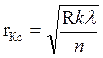. При отражении света от > плотной среды фаза волны света меняется на π, поэтому в отраженном свете центр колец будет темным. В проходящем свете такого изменения нет, поэтому центр колец светлый.

11. Принцип Гюйгенса-Френеля. Дифракция света. Метод зон Френеля.