Расчет канала связи. Расчет структурной схемы системы связи. Передача аналоговых сигналов методом ИКМ, страница 4

Одним из критериев помехоустойчивости может выступать так называемый минимум среднеквадратичного отклонения, т.е. максимальное приближение передаваемого и принимаемого сигналов. На языке математики этот критерий выглядит так:

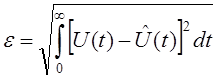                                            (4.1)

где  – исходный сигнал;

 – сигнал с помехой.

Однако эта формула больше подходит для непрерывных сигналов, т.к. оценивает квадрат разности напряжений, а квадрат напряжения это мощность. Оценка же мощностей двух дискретных сигналов не имеет смысла, т.к. при равной мощности сигнала могут быть совершенно различны.

Если мы имеем дело с дискретными сигналами, то, очевидно, что правильность приема сигнала сильно зависит от критерия принятия решения о том, какой же пришел сигнал: низкого уровня или высокого. Действительно в отдельные моменты времени значение выходного сигнала в условиях помех может не правильно описывать передаваемое. Однако в некоторых случаях даже человеческий глаз может различить, что здесь лишь помеха, а не смена полярности (см. рис. 4.1).

В таком случае необходимо вводить вероятностные оценки шума, правильности принимаемого сигнала и т.д. Обозначим 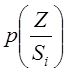 – вероятность того, что при значении сигнала на приемном конце равное  истинное значение передаваемого сигнала равно . Примем так же, что шумы в канале распределены по нормальному закону (Гауссово распределение), т.е. дифференциальная функция распределения (или плотность вероятности) имеет вид изображенный на рисунке 4.2

	Рисунок 4.1 Смесь сигнала и шума на входе приемника

 

	Рисунок 4.2 Плотность распределения вероятностей входных сигналов на приемном конце

 

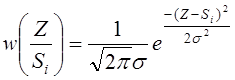                                          (4.2)

где  – среднеквадратичное отклонение.

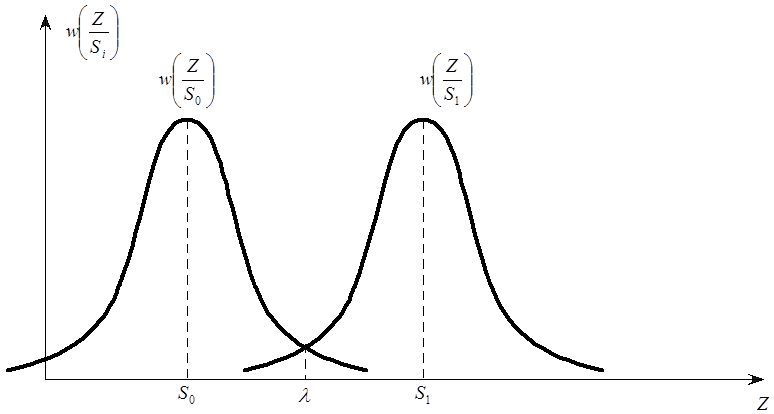
В таком случае на приемном конце будет ситуация, изображенная на рисунке 1.3.

Каждая точка кривой выражает вероятность того, что при заданном значении принимаемого сигнала передаваемый был , т.е. 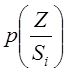. На рисунке видно, что кривые 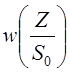 и 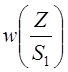 пересекаются при значении .

Критерий оценки, при котором сигнал с вероятностью больше  принимается равным единицы, а меньше  принимается равным нулю называется критерием Котельникова или критерием «идеального наблюдателя». Вероятность ошибки в таком случае определяется площадью лежащей ниже обеих прямых, и определяется как:

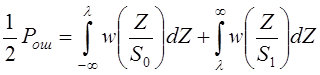                                       (4.3)

Куда бы мы не смещали  (соответственно меняя пределы интегрирования), вероятность ошибки будет лишь возрастать. Поэтому еще одно название данного критерия – критерий минимума вероятности ошибки.

Хотя руководствуясь данным критерием можно достичь минимальной ошибки его используют не всегда, а именно когда, например, вероятность ложного спокойствия – 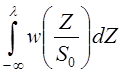 должна быть несопоставима меньше чем вероятность ложной тревоги –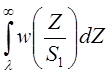 (например при обнаружении объекта противника радаром ближнего действия), в этом случае  сдвигают влево. При других обстоятельствах возможно уменьшение вероятности ложной тревоги.

Однако мы будем руководствоваться критерием «идеально наблюдателя». Найдем для этого случая вероятность ошибки с учетом (4.3) и (4.2) имеем:

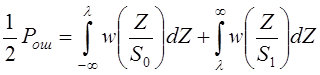
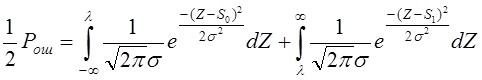
Учитывая свойства функции распределения вероятности, и произведя математические преобразования, получим:

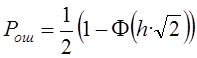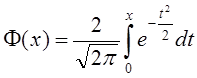, где           (4.4)

Функция  получила название функции Крампа, она табулирована.  в этой формуле это соотношение сигнал/шум находится как:

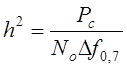                                                   (4.5)

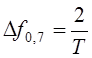                                                       (4.6)

Используя (4.4), (4.5) и (4.6) рассчитываем:

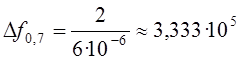 Гц

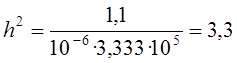
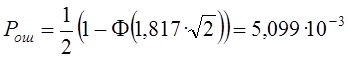
Таким образом, можно построить график зависимости вероятности ошибки от соотношения сигнал/шум (см. рисунок 4.3).