Расчет канала связи. Расчет структурной схемы системы связи. Передача аналоговых сигналов методом ИКМ, страница 3

Фазовая модуляция – один из видов угловой модуляции. При модуляции чистым тоном сигнал имеет вид:

                              (2.1)

где  – круговая или циклическая частота низкочастотного колебания;

 – несущая частота;

 – амплитуда сигнала;

 – начальная фаза высокочастотного колебания;

 – индекс фазовой модуляции

Максимальное значение  может достигнуть  (минимальное значение 0-мдуляции просто не будет). Тогда фаза сигнала  будет меняться в пределах от  до , т.е. максимально возможным образом. Если вместо косинусоиды  поставить любую другую нормированную функцию , зависящую от времени, то на приемном конце можно выделить  и получить, таким образом, фазовую модуляцию.

Однако брать в качестве  аналоговый (непрерывный) сигнал нецелесообразно, т.к. малейшее изменение фазы несущего высокочастотного сигнала приведет к неправильной трактовки  на выходе. В земных же условиях во-первых невозможно создать генератор частоты (у любого генератора существует некоторый разброс частот которые он излучает, что при данной трактовки принимаемого сигнала будет изменением фазы, т.е. ), во-вторых линия связи вносит свои фазовые искажения – в разные моменты времени различные условия окружающей среды – предугадать влажность, температуру, которые влияют на фазу приходящего сигнала просто невозможно.

В соответствие с вышесказанным в качестве  обычно берут дискретный сигнал, тогда фазовую модуляцию называют фазовой манипуляцией. В данной работе  принимает лишь два значения 0 или 1 (существуют модуляции в которых  принимает четыре значения: 0, 0.5, 1, 1.5, а так же смешанные виды модуляции), при этом . Таким образом, произведение  может принимать только два значения 0 и . Отличие этих сигналов на  объясняет аналогичное различие на между двумя выводами генератора высокой частоты  и .

Исходя из вышесказанного, запишем окончательное выражение для сигнала, передаваемого в линию:

                                    (2.2)

где  – последовательность нолей и единиц.

3 Выбор схемы демодулятора

Задачей демодулятора является выделение полезной информации из высокочастотного сигнала, описываемого формулой (2.2). Решим эту задачу с учетом наличия когерентного напряжения вида

                                          (3.1)

Для этого рассмотрим произведение :

Проинтегрируем правую и левую часть:

                     (3.2)

Второе слагаемое в формуле (3.2) окажется равным нулю при любых значениях , т.к. в подынтегральном выражении записано произведение двух ортогональных функций. Таким образом, выражение (3.2) примет вид:

                       (3.3)

Выражение (3.3) является основой для построения демодулятора, т.к.

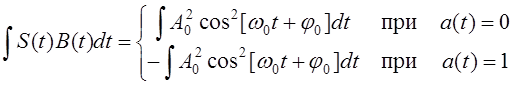                   (3.4)

Таким образом, схема демодулятора состоит (см. рис. 1.1) из умножителя, интегратора. Интегрирование следует производить за время, равное длительности единичного импульса. После интегратора, возможно, потребуется схема сдвига уровня, которая преобразует сигнал из последовательности положительных и отрицательных импульсов (см. выражение 3.6) в последовательность напряжений нулевого и высокого уровней. Для регулировки уровня напряжения, поступающего на ЦАП можно использовать усилитель (или делитель) напряжения сигнала с демодулятора, однако целесообразней подобрать соответствующий коэффициент усиления усилителя, который стоит перед демодулятором (чтобы не использовать дополнительных элементов, усложняющих схему и потребляющих энергию).

4 Расчет вероятности ошибки приемника

Что такое помехоустойчивость, и какими бывают помехи отмечено ранее. Здесь же нас интересуют критерии помехоустойчивости, т.е. встает вопрос о том, как же рассчитать вероятность ошибки в системе передачи информации?