Введение
Как научная дисциплина, теория распределения информции, образовалась на рубеже XIX – XX в.в., с связи резким увелечением числа коммутационных станций. Предметом ее изучения стали процессы обслуживания потоков сообщений в системах распределения информации.
Математическая модель системы распределения информации (теория телетрафика) включает следующие четыре основных элемента: входящий поток вызовы, систему распределения информации, характеристики качества и дисциплина обслуживания.
Основная цель теории телетрафика заключается в разработке методов оценки качества функционирования систем распределения информации. Поиск наиболее экономичных структур коммутационных схем, разработка принципов их построения и методов расчета пропускной способности становятся основным направлением теории. При этом выполнение условий по пропускной способности увязывается не только со стоимостью коммутационной схемы , но и с такими факторами, как надежность функционирования гибкость развития модульность построения, время передачи сообщения через коммутационное поле. Учитываются также требования предъявляемые к системе управления, программному обеспечению, устройствам памяти.
При анализе, синтезе и оптимизации систем распределения информации, кроме вероятностных методов используются комбинаторные и алгебраические методы. Основными методами решения задач являются аналитические, численные и метод статистического моделирования.
Аналитические методы позволяют решать задачи теории телетрафика в тех случаях когда структура системы, характеристики потока и дисциплины обслуживания относительно просты.
Наиболее универсальным методом который пригоден для решения задач практически любой сложности является метод статистического моделирования. Он заключается в построении математической модели системы, реализация которой осуществляется в виде программы для ЭВМ.
Задачи нормирования показателей качества по этапам соединения тесно связано с общей задачей оптимального построения систем коммутации. В теоретических исследованиях постепенно намечается переход к изучению процессов обслуживания всей системы, поиску оптимальных соотношений между численными характеристиками отдельных элементов системы. Разработка методов анализа и синтеза оптимальной структуры системы коммутации в целом – несущая задача теории. Необходимость ее решения диктуется произошедшей интеграцией систем передачи, коммутации и средств вычислительной техники, начавшейся интеграцией сете электросвязи, различного назначения, появившейся возможностью передачи по единой сети связи сообщений различного вида.
Развитие электронной коммутационной техники поставило перед теорией телетрафика сложные задачи синтеза в которых требуется определить структурные параметры коммутационных систем, при заданных потоках, дисциплине и качестве обслуживания.
Цель данного курсового проекта рассмотреть теоретические вопросы по дисциплине “теория телетрафика” и выполнить ряд задач по данному курсу, а также спроектировать схемы включения неполнодоступного пучка.
Задача 1
На коммутационную
систему поступает поток вызовов, создающий нагрузку 4,5 Эрл. Определить
вероятность поступления ровно i вызовов
![]() (i=0, 1, 2, …, 9) при примитивном
потоке от 9 источников и
(i=0, 1, 2, …, 9) при примитивном
потоке от 9 источников и ![]() (i=0, 1, 2, …, j, …) при простейшем потоке вызовов.
Построить кривые распределения вероятностей
(i=0, 1, 2, …, j, …) при простейшем потоке вызовов.
Построить кривые распределения вероятностей ![]() и
произвести сравнения полученых результатов.
и
произвести сравнения полученых результатов.
Простейший поток определяется распределением Паусона:
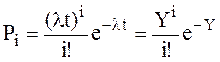 . (1.1)
. (1.1)
Найдем вероятность отсуствия поступления вызовов:
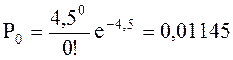 ;
;
Дальнейшие значения вероятностей можно рассчитать по рекуррентной формуле:
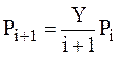 . (1.2)
. (1.2)
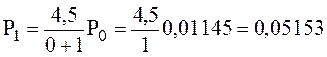 ;
;
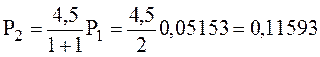 ;
;
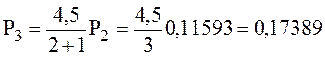 ;
;
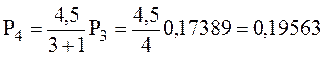 ;
;
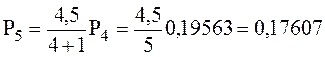 ;
;
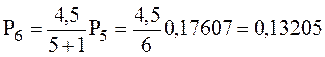 ;
;
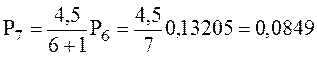 ;
;
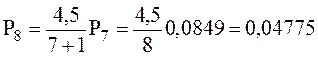 ;
;
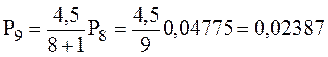 .
.
Примитивный поток описывается распределнием Бернули:
![]() , (1.3)
, (1.3)
где а – нагрузка от одного источника:
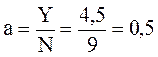 Эрл. (1.4)
Эрл. (1.4)
Найдем вероятность отсуствия поступления вызовов:
![]() .
.
Дальнейшие значения вероятностей можно рассчитать по рекуррентной формуле:
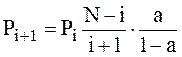 . (1.5)
. (1.5)
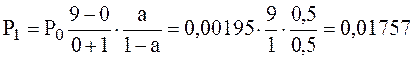 ;
;
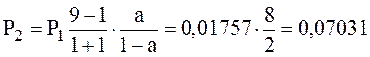 ;
;
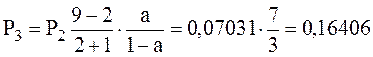 ;
;
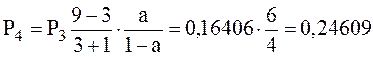 ;
;
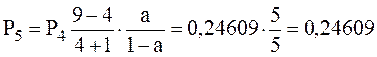 ;
;
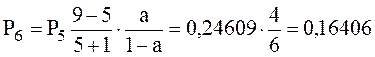 ;
;
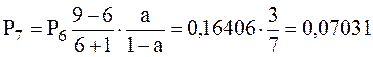 ;
;
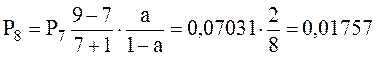 ;
;
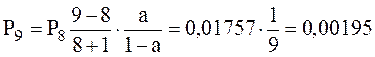 .
.
Полученые результаты отобразим на общем графике (рисунок 1.1).
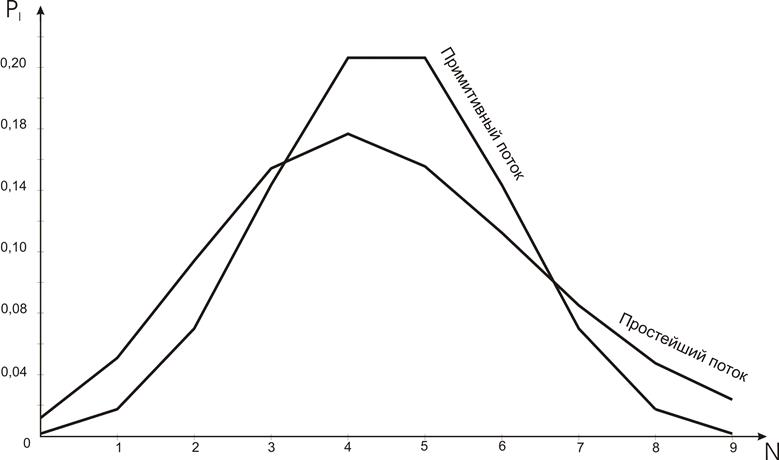
Рисунок 1.1 – Кривые распределения вероятностей
Вывод: Простейший
поток является потоком чистой случайности, поэтому кривая распределения
получилась близкая к нормальному закону распределения с максимумом в точке ![]() . При этом вероятность
поступления вызовов на участке i = 3…6 в
простейшем потоке меньше, чем в примитивном потоке. При примитивном потоке
учитывается последействие, причем при малом числе N последействие высоко, что и можно
увидить на графиках. При увеличении N до влечины 300…500, примитивный поток можно заменить на более простую модель
простейшего потока.
. При этом вероятность
поступления вызовов на участке i = 3…6 в
простейшем потоке меньше, чем в примитивном потоке. При примитивном потоке
учитывается последействие, причем при малом числе N последействие высоко, что и можно
увидить на графиках. При увеличении N до влечины 300…500, примитивный поток можно заменить на более простую модель
простейшего потока.
Задача 2
В блок абонентского искания (БАИ) цифровой системы коммутации типа ДХ – 200 включено 3904 абонентских линий.
Определить поступающую на БАИ нагрузку, если среднее число вызовов от одного абонента С = 2 выз/ч, среднее время разговора Т = 140 с, доля вызовов закончившихся разговоров РP = 0,7. Нумерация в сети шестизначная.
Нагрузка является количественным показателем поступающего потока
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.