Теперь определим по рисунку 1 приложения 3 [2]
значения ![]() ,
зная
,
зная
![]() ,
и Yм
= 0,3 Эрл, при t = 4
,
и Yм
= 0,3 Эрл, при t = 4
![]()
Ответ: Вероятность ожидания свыше допустимого
времени tд = 3,6 с ![]() среднее
время ожидания задержанных вызовов
среднее
время ожидания задержанных вызовов ![]() .
.
Задача 5
Неполнодоступный пучок линий в однозвенной системе с отказами обслуживает нагрузку Y = 35 Эрланг при доступности d = 20. Определить ёмкости пучка v при двух значениях потерь Р1 = 2 %º и Р2 = 2 %º. Сравнить полученные результаты. Рассчитать структурные параметры и составить неполнодоступную схему, определить вероятность потерь.
Решение
Для упрощения расчетов используем формулу:
![]()
где a и b - коэффициенты, зависящие от доступности d и потерь сообщений Р:
Определим их для известной доступности d и известной вероятности потерь сообщений.
Имеем:
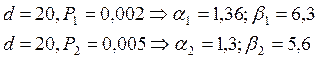
тогда
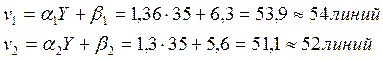
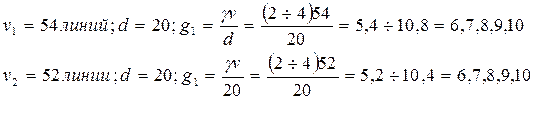
Рассчитаем структурные параметры равномерной неполнодоступной
схемы ступенчатого включения для ![]() ;
;
![]() и
и
![]() .
.
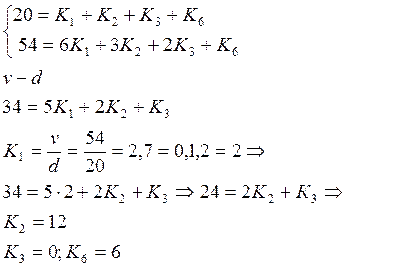
Исходя из рассчитанных параметров, строим неполнодоступную схему и составим матрицу связности, для g1 = 6 , которая вместе с матрицей связности представлена на рисунке 5.1. Так как разница между двумя любыми элементами матрицы связности не превышает по абсолютному значению единицу, то это говорит о том что, что неполнодоступная схема составлена правильно.


|
Рассчитаем структурные параметры равномерной неполнодоступной схемы цилиндров для g=6 и d=20.
При заданных: ![]() и
d необходимо определить точки коммутации, принадлежащие разным группам и
различным шагам искания путем запараллеливания по r и г+1,
где r определяется по формуле:
и
d необходимо определить точки коммутации, принадлежащие разным группам и
различным шагам искания путем запараллеливания по r и г+1,
где r определяется по формуле:
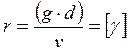
Для определения соответствующих точек
коммутации необходимо определить число линий ![]() ,
полученных путем запараллеливания по (r+1) точку и число линий
,
полученных путем запараллеливания по (r+1) точку и число линий ![]() ,
полученных путем запараллеливания по r точек.
,
полученных путем запараллеливания по r точек.
Эти значения определяются по следующим соотношениям:
![]()
![]()
![]()
Для определения этих значений удобнее, если коэффициент уплотнения представить в целой и дробной части, в которой не производится сокращение:
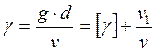
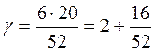
![]() ;
; ![]()
![]() для
для
![]()
![]() ;
;
![]() ;
;
![]() для
для
![]()
Рассчитаем число шаговых цилиндров:
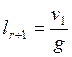 ;
; 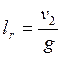
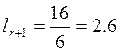
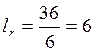
Примем ![]() ;
;
![]()
![]()
![]()
Нам не хватает 4 линии, получим их путем запараллеливания оставшихся выходов с наименьшим нарушением всех указываемых требований.
По рассчитанным параметрам построим матрицу связности и неполнодоступную схему (рис. 5.2).
![]()


Рисунок- 5.2-Неполнодоступная схема цилиндров и матрица связности.
Задача 6.
Нагрузку, поступающая на ступень ГИ АТСК, обслуживается в данном направлении пучком линий с доступностью Квд = 20 при потерях Р = 0,005. Нагрузка на один вход ступени а = 0,5 Эрланг, нагрузка в направлении Y = 25 Эрланг. Определить методом эффективной доступности ёмкость пучка v при установки на ступени блоков 60*80*400 и 80*120*400. Сравнить полученные результаты.
Решение.
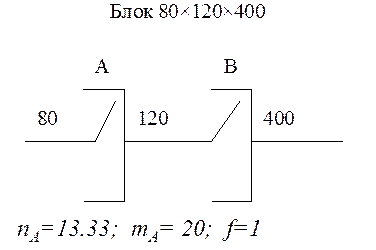 |
|||
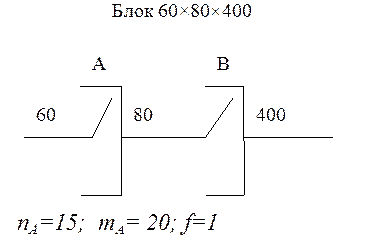 |
|||
Рисунок 6.1 Рисунок 6.2
Задача решается по методу эффективной доступности, пригодному как для полнодоступных так и для неполнодоступных двухзвенных схем. Он основан на переменной доступности. Когда нет занятых соединительных путей (линий), каждому входу 1 ступени ГИ доступен любой выход требуемого входа 2 ступени, доступность выходов данного направления максимальна (все выходы доступны).
Для схем с расширением или
сжатия ![]() минимальная
доступность:
минимальная
доступность:
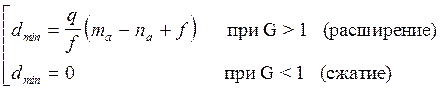
где
q – число выходов из одного коммутатора в направлении
искания: 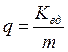 .
.
В процессе работы двухзвенной схемы в режиме ГИ доступность выходов di меняется в пределах:
dmin £di£dmax
Для двухзвенной схемы существует эквивалентная схема (по потерям) однозвенного включения НПД. Доступность такой схемы называется эффективной доступностью dэ. Определяется формулой:
dmin < dэ < dmax
![]()
где ![]() -
коэффициент, определяемый зависимостью потерь от доступности и распределением
вероятностей доступности Wi;
-
коэффициент, определяемый зависимостью потерь от доступности и распределением
вероятностей доступности Wi;
![]() -
математическое ожидание доступности.
-
математическое ожидание доступности.
![]() =0.7
=0.7
где f - связность.
![]() при f =1
при f =1
где Ym - интенсивность нагрузки, обслуженной m ПЛ, рассчитывается по формуле:
Ym = ana ,
где а = нагрузка, создаваемая одним источником в единицу времени (часозанятие)
ma и nа - структурные параметры коммутатора.
Расчёт.
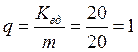
![]() Эрл
Эрл
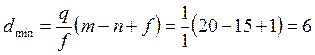
![]()
![]()
По таблице из приложения 4 [2] выбираем ![]() и
и
![]() :
:
![]()
![]() выбираем
v =44
выбираем
v =44
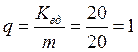
![]() Эрл
Эрл
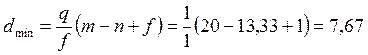
![]()
![]()
По таблице из приложения 4 [2] выбираем ![]() и
и
![]() :
:
![]()
![]() выбираем
v = 43
выбираем
v = 43
Вывод: С увеличением числа промежуточных линий, число требуемых
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.