Неполнодоступная система построена правильно, так как разница между двумя элементами столбца не превышает по абсолютной величине 1, т.е. матрица удовлетворяет требованиям, обеспечивающим одинаковую связность каждой нагрузочной группы друг с другом и характеризуется одинаковым влиянием друг на друга, и соответствующим одинаковым распределением нагрузки по различным нагрузочным группам.
При нагрузки У=20 эрл., доступности d=12 и вероятности Р1=0,005 мы получили ёмкость пучка больше, чем при вероятности Р2=0,01.
ЗАДАЧА 6.
Нагрузка, поступающая на ступень ГИ АТСК, обслуживается в данном направлении пучком линий с доступностью Квq=20 при потерях Р=0,005. Нагрузка на один вход ступени а=0,43 эрл, нагрузка в направлении У=23эрл.
Определить методом эффективной
доступности ёмкость пучка U при установке
на ступень блоков 60
и 
. Сравнить
полученные результаты. По заданию также дано q = 0,7, nA=13.33,
mA=KB=20, f=1 для
блока и
nA=15, mA= KB=20, f=1 для блока 60.
Решение.
Определим нагрузку на ступень блока по формуле:
Уma = a×·nA
( 14 )
Уma= 
эрл.
Число нагрузочных групп найдем по формуле:
(
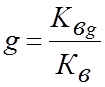15 )
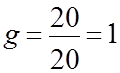
Теперь определим минимальную доступность:
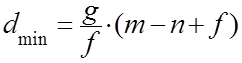(16 )
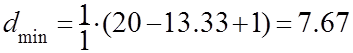
Следующим определим математическое ожидание доступности:
(17 )
Эффективную доступность определим по формуле:
q
( 18 )
Из приложения 4 по известным значениям Р=0,005 и dэ=12 определим значения коэффициентов a и b:
a =1,55 и b=3,9
Тогда ёмкость пучка найдём по формуле:
линия.
Тоже самое определим для блока 60:.
Уma рассчитаем по формуле (14)
Уma= 
эрл.
По формуле (15) найдем g:
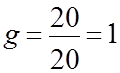
Минимальную доступность определим по формуле (16 ):
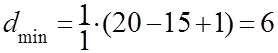
Математическое ожидание доступности по формуле (17):
Эффективную доступность определим по формуле ( 18 ):
Из приложения 4 по известным значениям Р=0,005 и dэ=11 определим значения коэффициентов a и b:
a = 1,62 и b=3,6
линия
Вывод, при одинаковой нагрузке на ступени ГИ АТСК ёмкость пучка на ступени блоков 60*80*400 и 80*120*400 различна и составляет 41 и 40 линию соответственно. Получается, что более выгоднее устанавливать блоки 80*120*400, т.к. для них требуется меньшее число линий.
ЗАДАЧА 7.
На вход ступени БСЛ АТСКЭ поступает нагрузка по двум пучкам линий, математическое ожидание которой У1=33 эрл иУ2=57 эрл. На выходе ступени объединенная нагрузка распределяется по направления пропорционально коэффициентам Кi ( К1=0,1; К2=0,17; К3=0,27; К4=0,46 )
Определить расчётное значение нагрузки каждого направления и относительное отклонение расчётного значения нагрузки от её математического ожидания. По результатам сделать вывод.
Решение.
Так как в разные дни, недели, месяцы, года в ЧНН нагрузка изменяется постоянно это изменение приводит к изменению качественных показателей качества обслуживания, которые ухудшаются. Чтобы качественные показатели качества обслуживания не превышали заданных значений, необходимо использовать такую нагрузку, при которой с максимальной вероятностью качественные показатели оставались постоянными. Такой нагрузкой является расчетная нагрузка. Поэтому, при объединении и разъединении потоков, нагрузки на различных ступенях искания телефонных сетей величины расчетных нагрузок должны определяться в последовательности: в случае объединения потоков нагрузки - надо найти математическое ожидание суммарной нагрузки, как сумму математических ожиданий объединяемых нагрузок, а затем перейти к расчётному значению нагрузки для определения числа устройств обслуживающих суммарную нагрузку:
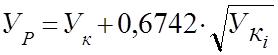(19)
где – Ук- математическое ожидание;
- нагрузка в i-ом
направлении.
При разделении нагрузки на выходе ступеней искания общей нагрузки по направлениям следует определить математическое ожидание данного направления по формуле:
(20)
Затем распределить эту нагрузку по направлениям. В соответствии для каждого направления надо найти Ур, по отношению к которым определено число соединительных линий или коммутационных устройств.
Найдем общую нагрузку:
Уобщ. =У1+У2 (21)
Уобщ. =33+57=90 эрл.
Нагрузку в каждом направлении найдём по формуле:
Укi =У×Кi (22)
УК1=90×0,1=9 эрл.
УК2=90×0,17=15,3 эрл.
Ук3 =90×0,27=24,3 эрл.
УК4=90×0,46=41,4 эрл.
Теперь по формуле (19) найдем УР:
УР1=
эрл.
УР2=
эрл.
УР3=
эрл.
УР4=
эрл.
Математическое ожидание по отношению к УР найдём по формуле (20):
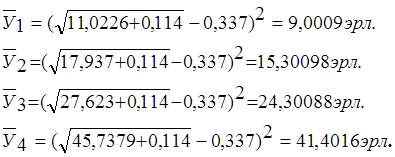
Величину относительного отклонения расчетной нагрузки от ёё математического ожидания нагрузки найдём по формуле:
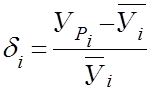(23)
где 
- расчетное
значение нагрузки в направлении i;
-
математическое ожидание.
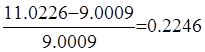
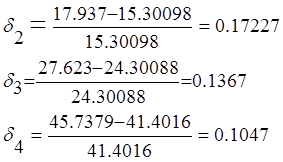
Сравнивая полученные результаты можно сделать вывод о том, что при малых нагрузках относительные колебания получаются значительными, а при больших – наименьшие. Следовательно качественные характеристики более стабильны при обслуживании малых нагрузок.
Заключение.
Современное состояние связи, телекоммуникаций и информатики характеризуется широким спектром потребностей в различных видах техники и характере передаваемой информации. Очень многие отрасли и виды деятельности человека на данный момент немыслимы без современного обеспечения.
Для передачи всех видов информации с учётом сегодняшнего дня создаётся широкополосная цифровая сеть интегрального обслуживания, в которой в качестве основного способа передачи информации предполагается использовать асинхронный способ. В широкополосных сетях новыми возможностями становятся такие услуги как: кабельное телевидение, высокоскоростная передача данных, видеотелефон, высокоскоростной цветной телефакс.
Таким образом, возникает специфика в задачах теории телетрафика, относящихся к асинхронным интегральным сетям. Характерными особенностями задач теории телетрафика, появившимися в связи с использованием новых технических средств передачи информации на сетях связи, является необходимость многоуровневого рассмотрения задач. Поэтому, без знания основ предмета теория телетрафика нельзя создать
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
