Формирование аналогового телевизионного сигнала. Тракт формирования телевизионного сигнала. Упрощённые структурные схемы видеоусилительного тракта ТВ центра для передачи изображений, страница 7

                                                             ,                                                              (4.2)

Из графика рисунка 4.3 следует, что при соответствующем стандарту числе элементов разложения вдоль строк () амплитуда сигнала составляет от максимума только .

Число чёрно-белых элементов m, расположенных вдоль строки, и частота  телевизионного сигнала, соответствующего передаче этих элементов при движении электронного луча вдоль строки, определяются в соответствии с рисунком 4.3 б выражением:

,                                                                       (4.3) где  - время развёртки   одной строки (обычно = 0,86;мкс).

Апертурные корректоры выполняются по двум распространенным схемам. Одна из них основана на применении дифференцирующих цепей. Сущность метода дифференциальной апертурной коррекции заключается в следующем. Апертурная характеристика аппроксимируется следующей чётной функцией:

                                                               ,                                                 (4.4)

где - частота, при которой амплитуда сигнала уменьшается в е раз (е — основание натуральных логарифмов). Графически функция (4.4) изображена на рисунке 4.4 в.

Рисунок 4.2 - Апертурные искажения резких переходов яркости

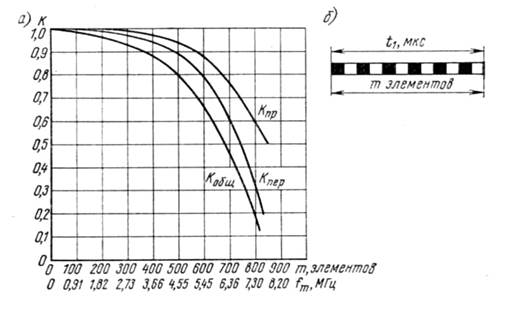
Рисунок 4.3 - Апертурные искажения, вносимые приёмной и передающей трубками: а) апертурные характеристики; б) к определению связи между числом элементов и частотой их следования

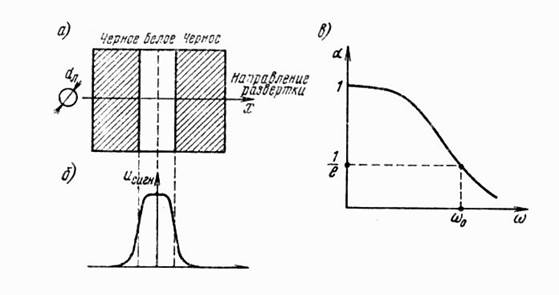
Рисунок 4.4 - Образование сигнала при симметричной форме считывающего луча:  а) передаваемое изображение; б) форма видеосигнала; в) аппроксимирующая функция 

Выражение (4.4) может быть представлено в виде:

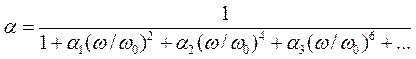,                             (4.5)

где 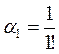, , 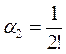 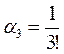и т. д.

Корректирующее устройство должно иметь обратную частотную характеристику вида:

                                                                                           (4.6)

Дифференциальная апертурная коррекция сводится к синтезу частотной характеристики,   описываемой  выражением  (4.6).   Из  него  видно,  что  общая частотная характеристика  может быть представлена как сумма частотных характеристик , и т. д. Характеристики такого типа могут быть получены при помощи обычных дифференцирующих цепей. Частотная характеристика однозвенной дифференцирующей цепи (рисунок 4.5 а) определяется выражением:

.                            (4.7)

При соответствующем выборе постоянной времени RC выполняется следующее неравенство  и

                                                               (4.8) Фазовая характеристика:

                                                                                                            (4.9)

При выполнении неравенства получим  Частотная и фазовая характеристики однозвенной дифференцирующей цепи изображены на рисунке 4.5    (б и в).

На практике обычно используются более сложные дифференцирующие цепи, обеспечивающие за счёт применения дополнительных элементов больший коэффициент передачи при сохранении линейной фазовой характеристики. Применяются также цепи двойного дифференцирования, позволяющие получить сразу сигнал второй производной.

Структурная схема апертурного корректора дифференциального типа, переходная характеристика и принципиальная схема формирователя второй производной  представлены на рисунке 4.6 (соответственно а, б, в).

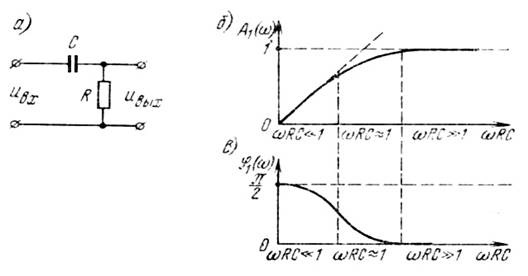
Рисунок 4.5 - Дифференцирующая цепь:   а) принципиальная схема; б) частотная характеристика; в) фазовая характеристика

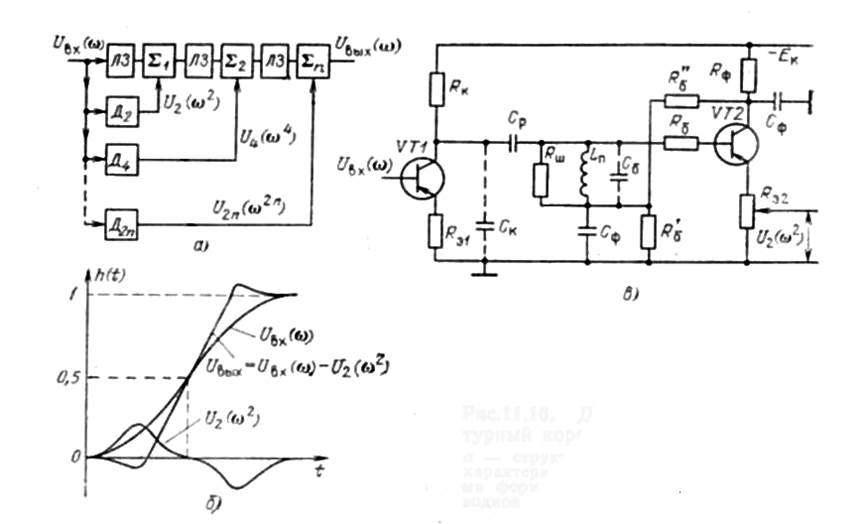
Рисунок 4.6 - Дифференциальный апертурный корректор: а) структурная схема; б) переходная характеристика; в) принципиальная схема формирователя второй производной 

В сумматорах ,  и  входной сигнал складывается с сигналами чётных производных, которые формируются дифференцирующими цепочками Д₁, Д₂, ... Д_n. Фазовые сдвиги, возникающие при формировании корректирующих сигналов, компенсируются с помощью линий задержки ЛЗ. На практике часто ограничиваются использованием сигнала второй или четвёртой производной.