Применение ЭВМ на отдельных этапах проектирования электронных схем. Этап анализа и оптимизации параметров схемы, страница 6

Очевидно, оного уравнения (3.1) недостаточно для расчета , т.к. в правую часть уравнения входит неизвестное . Необходимо дополнительное уравнение, которое позволит найти значение вектора состояния . Это уравнение получим с помощью следующих рассуждений. Напряжение на каждом индуктивном элементе 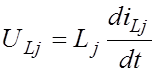 и ток каждого емкостного элемента 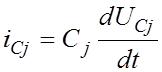 определяется как вектором независимых источников , так и вектором состояния . Соответствующие рассуждения можно провести для каждого реактивного элемента. Следовательно, производная от вектора состояния связана линейной зависимостью с вектором состояния и вектором независимых источников вида:

,

(3.2)

где -матричные коэффициенты, значение которых определяется топологией цепи и параметрами схемы.

Данное уравнение называется уравнением состояния. Порядок этого уравнения (число уравнений в матричном уравнении (3.2)) равен числу элементов вектора , т.е. числу реактивных элементов в схеме. Интегрируя эту систему уравнений (вектор считается известным), можно определить все элементы вектора состояния . Подставляя найденные значения  в (3.1), можно рассчитать токи резисторов .

Уравнение выхода. Очевидно в схеме бывает обозначен выход, отклик на котором представляет интерес. Этим откликом может быть напряжение  между какими-либо узлами схемы, либо как  в некоторой ветви. Не корректируя вид отклика в дальнейшем будем обозначать его как . Так как R-цепь находится под воздействием двух типов источников – вектора независимых источников  и вектора состояния, то  можно выразить линейной зависимостью от этих векторов:

,

(3.3)

где -коэффициенты, определяемые параметрами и топологией цепи.

Так как схема имеет один выход, то  является скалярной, а не векторной величиной.

Совокупность уравнений (3.1)-(3.3) образует математическую модель цепи, на основании которой может быть выполнен анализ любой цепи.

3.3 Алгоритм вычисления коэффициентов  и  уравнения токов резисторов

Воспользуемся топологическими уравнениями цепи (2.2) и (2.5):

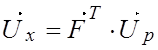
Запишем уравнение с использованием матрицы главных сечений для токов резистивных ребер  и напряжений резистивных хорд .

Для этого воспользуемся записью матрицы  через подматрицы (2.6). Нас интересуют не вся матрица , а только её часть, относящаяся к строке  и столбцу .

	(3.4)
	(3.5)

Дополним эти топологические уравнения компонентными уравнениями для резистивных элементов, определяющими по закону Ома зависимость между напряжениями и током на этих элементах:

, ,

(3.6)

где  и -матрицы сопротивлений резистивных ребер и резистивных хорд.

В этих матрицах элементы, расположенные в главной диагонали – сопротивления соответствующих резистивных элементов. Остальные элементы этих матриц равны нулю.

Выразим в (3.5) напряжения на резистивных элементах через токи на этих элементах, используя соотношения (3.6), после чего все члены, содержащие токи резистивных элементов перенесем в левые части равенств.

Объединим эти уравнения в одно матричное уравнение:

(3.7)

С учетом введенных обозначений уравнение примет вид:

Поделив обе части последнего уравнения на , получим:

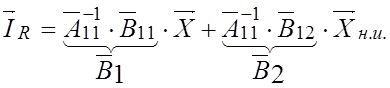
Сравнив (3.7) с (3.1), делаем вывод:

,

(3.9)

Значения матриц , ,  определены в (3.7).

Пример 3.1. Рассчитать матричные коэффициенты  и  уравнения токов резисторов для схемы (рисунок 2.1).

Входящие в уравнение (3.1) векторы:

; ;

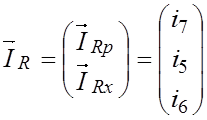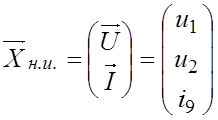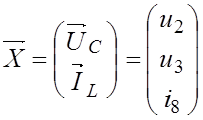
Матрица сопротивлений резистивных элементов с учетом масштабного коэффициента :

;

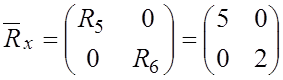
Матрица главных сечений  равна (2.3):

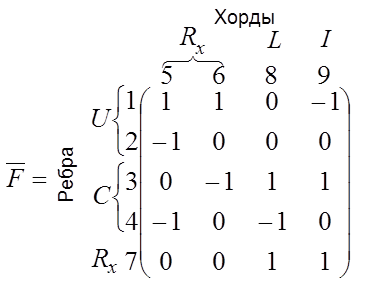
Соответствующие ей подматрицы равны:

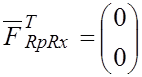; -транспонированная матрица;

; ;

; ;

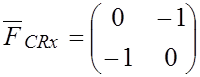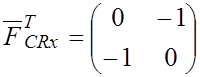
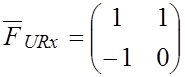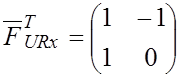
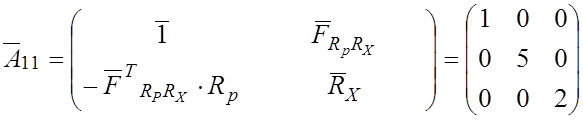
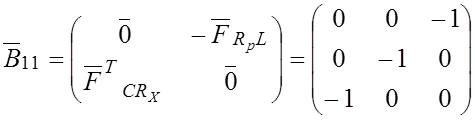
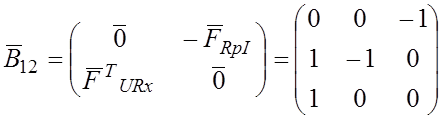
Для диагональной матрицы  обратная матрица  находится заменой в главной диагонали элементов на их обратное значение. Таким образом:

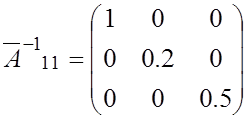
Теперь можно определить значение коэффициентов уравнений токов резисторов:

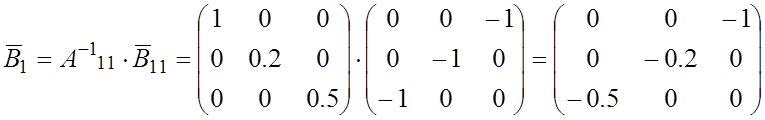
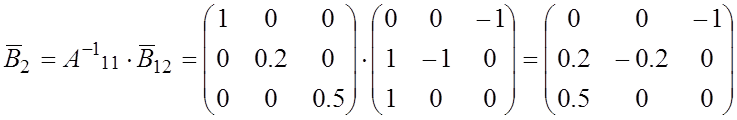
Следовательно, уравнение токов резисторов (3.1) запишется для рассматриваемой цепи следующим образом:

(3.10)

Или в виде системы линейных уравнений:

(3.11)

Количество уравнений равно числу резисторов в схеме.