Применение ЭВМ на отдельных этапах проектирования электронных схем. Этап анализа и оптимизации параметров схемы, страница 4

Здесь строки принадлежат ребрам, столбцы – хордам графа. Заметим, что взятые с обратным знаком элементы строки представляют собой коэффициенты, связывающие ток соответствующего этой строке ребра с токами хорд.

(2.3)

Обратим внимание еще на одну особенность матрицы . Ненулевые элементы в столбце хорды показывают, с какими ребрами данная хорда образует замкнутый контур. При этом элементы столбца представляют собой коэффициенты, с помощью которых напряжение хорд выражается через напряжение ребер. Таким образом, для рассматриваемой цепи имеем:

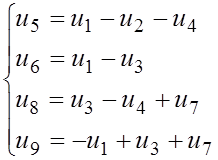
Это полная система независимых уравнений по второму закону Кирхгоффа (ЗКН). Систему уравнений представим в матричной форме:

(2.4)

С использованием полученных обозначений:

,

(2.5)

где -вектор напряжений хорд;

-вектор напряжений ребер;

-транспонированная матрица .

Уравнение (2.5) представляет собой топологическое уравнение по ЗКН для произвольной цепи.

2.4 Матрица главных сечений произвольной схемы

Строки и столбцы матрицы  можно сгруппировать по типам элементов, к которым они принадлежат так, как это сделано в (2.3), где -строки источников напряжений, -строки емкостных ребер; -строки резистивных ребер, -столбцы резистивных хорд; -столбцы индуктивных хорд, -столбцы источников тока. При этом матрица  может быть разбита на подматрицы и представлена в виде:

(2.6)

Здесь индексы у подматриц указывают на типы ветвей, к которым принадлежат строки и столбцы подматриц. Такое представление является общей формой матрицы  для произвольной цепи.

Выражение (2.6) предполагает, что дерево графа выбирается таким образом, чтобы все ветви с источниками напряжений и емкостными элементами принадлежали дереву (т.е. являлись ребрами), а все ветви с индуктивностями и источниками токов принадлежали дополнению дерева (т.е. являлись бы хордами), резисторы оказываются распределенными между деревом и дополнением дерева.

2.5 Алгоритм формирования матрицы главных сечений

Формирование матрицы главных сечений  производится в два этапа. На первом этапе по введенным в ЭВМ данным цепи формируется так называемая структурная матрица  (другое часто встречающееся в литературе название – матрица инциденций). На следующем этапе путем преобразований, проводимых над структурной матрицей, получают матрицу .

Рассмотрим построение структурной матрицы. Составим матрицу следующим образом. Припишем столбцы матрицы ветвям графа, строки – его узлам. Дадим элементам  этой матрицы следующие значения:

Для графа, изображенного на рисунке 2.2б получим:

Каждая -я строка такой матрицы показывает, какие ветви подключены к -му узлу и каково их направление относительно узла, а каждый -й столбец показывает, с какими узлами соединена -я ветвь и направление этой ветви.

Так как каждая ветвь подключена к двум узлам, то в любом из столбцов матрицы  имеется только два ненулевых элемента, один из которых +1, другой –1.

В связи с этим значения элементов одной из строк всегда могут быть определены через элементы других строк, поэтому одну из строк можно вычеркнуть. Вычеркивая в  последнюю строку, получают следующую матрицу:

(2.7)

Эта матрица дает топологическое описание цепи и называется структурной матрицей.

Так как строки матрицы  указывают ветви, подключенные к соответствующим узлам и их направление относительно узлов, то, умножая строки матрицы на вектор токов ветвей , будем иметь алгебраическую сумму токов в узлах, которая по ЗКТ равна нулю. Следовательно:

(2.8)

Действительно, подставим в (2.8) данные цепи, изображенной на рисунке 2.1:

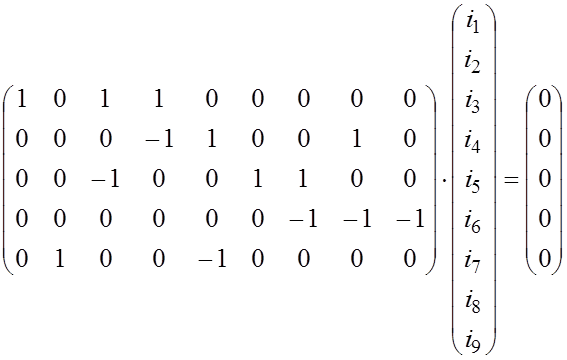
Эта матричная запись соответствует следующей системе уравнений:

(2.9)

Для получения матрицы  необходимо данную систему уравнений решить относительно токов ребер. Эта операция может быть выполнена методом исключения переменных: из всех уравнений, кроме первого исключается ток , затем из всех уравнений, кроме второго, исключается ток  и т.д. Проведение операции исключения переменных преобразует матрицу  таким образом, что в левой части образуется единичная матрица , а правая часть представляет искомую матрицу главных сечений . Алгоритм получения матрицы  из  можно представить следующей последовательностью шагов: