Применение ЭВМ на отдельных этапах проектирования электронных схем. Этап анализа и оптимизации параметров схемы, страница 5

1)  Задается =1, где  - номер столбца.

2)  Исключают из рассмотрения первые (-1) строк и столбцов, последовательно просматривая оставшуюся часть матрицы по столбцам, ищут первый ненулевой элемент. Пусть этот элемент .

3)  Если , то -й столбец ставят на -е место, столбцы от -го до (-1)-го сдвигают вправо.

4)  Если , то меняются местами -я и -я строки.

5)  Если , то элементы -й строки умножаются на минус 1.

6)  Если в -м столбце кроме элемента  имеются дополнительные ненулевые элементы, то они устраняются путем прибавления или вычитания -й строки к строкам этих элементов.

7)  Задается =+1. Если  (где - число узлов схемы), то идти к шагу 2; в противном случае  правых столбцов матрицы есть искомая матрица  ( - число ветвей схемы).

Используем данный алгоритм для получения матрицы  из структурной матрицы .

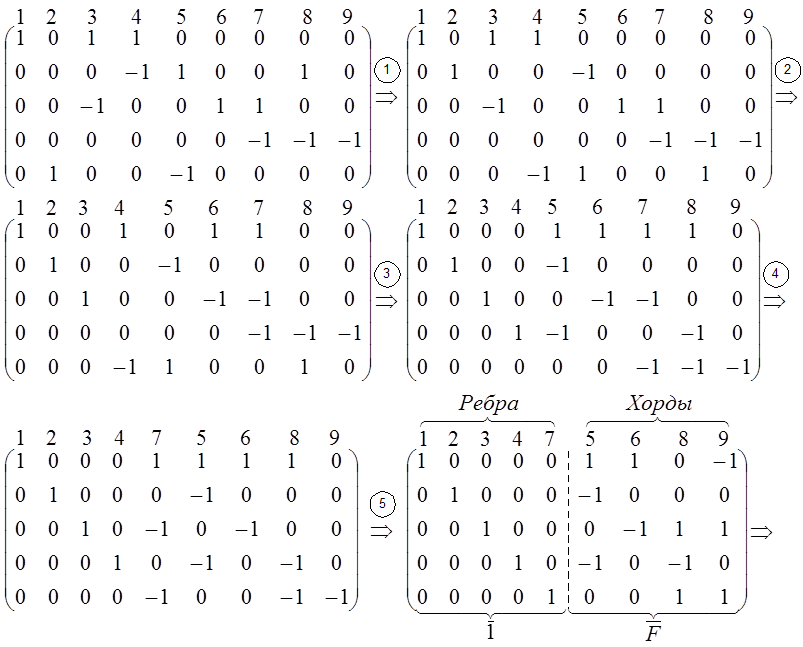
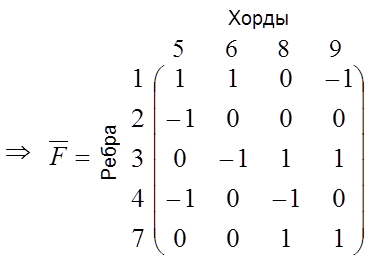
Первая матрица представляет собой исходную матрицу .

1 шаг: поменяем местами 2-ю и 5-ю строки;

2 шаг: поменяем знак 3-й строки и из 1-й строки вычтем 3-ю, чтобы устранить ненулевой элемент в 3-м столбце;

3 шаг: поменяем местами 5-ю и 4-ю строки; изменим знак 4-й строки и из 1-й строки вычтем 4-ю строку;

4 шаг: т.к. в 5-м столбце не оказалось необходимого элемента 1, на место 5-го столбца поставим 7-й столбец, столбцы 5-й и 6-й сдвинем вправо;

5 шаг: поменяем знак в 5-й строке, вычтем из 1-й строки 5-ю строку, прибавим к 3-й строке 5-ю строку, чтобы устранить ненулевые элементы в 5-м столбце.

В результате всех преобразований в левой части получена единичная матрица , а правая часть представляет собой матрицу главных сечений . Ветви с номерами 1,2,3,4,7 являются ребрами, а ветви 5,6,8,9 – хордами. Как видим, полученная матрица  совпала с матрицей (2.3).

3 Формирование математической модели линейной цепи

3.1 Метод переменных состояния

В задачах исследования и разработок, типичных для радиотехники и связи используют метод переменных состояния. Кроме того, метод переменных состояния имеет широкое применение при анализе различных систем и сетей связи. Поясним суть этого метода.

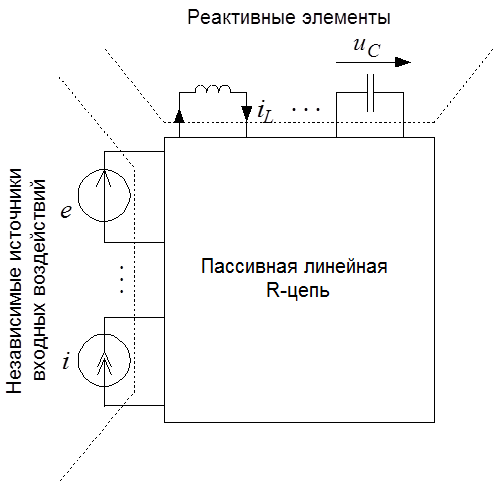
Вынесем за пределы анализируемой цепи (рисунок 3.1а) независимые источники (источники входных воздействий – источники питания и входных сигналов) и реактивные элементы.

а)

б)

в)

Рисунок 3.1

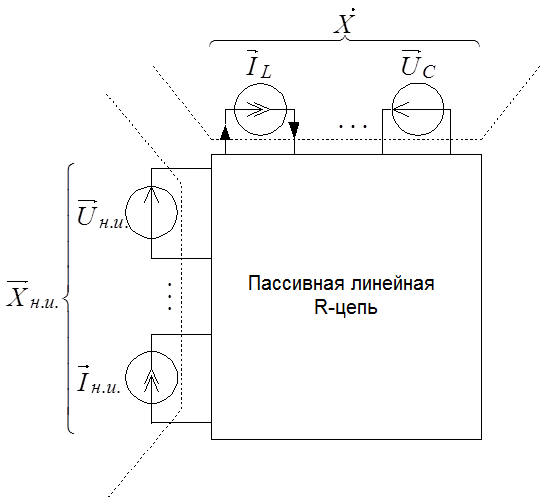
При этом будем считать, что анализируемая схема не содержит управляемых источников. Оставшаяся часть схемы после вынесения из неё указанных элементов (рисунок 3.1б) будет представлять собой пассивную линейную R-цепь. Очевидно, токи (напряжения) в элементах R-цепи не изменят своих значений, если индуктивные элементы заменить источниками тока, а емкостные – источниками напряжения (рисунок 3.1в). При этом источники, замещающие реактивные элементы, должны быть такими, чтобы их токи и напряжения в каждый момент времени имели те же значения, что и токи и напряжения соответствующих элементов.

В такой преобразованной схеме линейная R-цепь оказывается под воздействием источников двух типов: независимых источников, представленных вектором 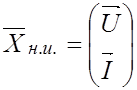, и источников замещения реактивных элементов, которые представлены вектором состояния .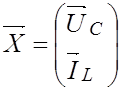

При известных напряжениях и токах независимых источников напряжения и токи на всех элементах схемы в любой момент времени определяется вектором состояния для этого момента времени. Такой метод анализа схемы с описанием анализируемых процессов с помощью уравнений, в которых в качестве независимой переменной используется вектор переменных состояния называется методом переменных состояния.

3.2 Структура уравнений математической модели линейной цепи

Поскольку пассивная R-цепь находится под воздействием двух типов источников  и , то в каждый момент времени токи в R-цепи будут линейно связаны с вектором независимых источников  и вектором состояния . Эта зависимость может быть выражена линейным уравнением вида:

,

(3.1)

где 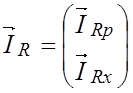-токи резистивных ребер и резистивных хорд;

Матричное уравнение (3.1) называется уравнением токов резисторов. Порядок этого уравнения (число уравнений в матричном уравнении (3.1)) равен числу резистивных элементов в схеме. Коэффициенты  и  - матричные коэффициенты, значения которых определяются топологией цепи и параметрами резистивных элементов R-цепи.