Неопределенный интеграл. Определенный интеграл. Подстановка к уравнению. Тип дифференциального уравнения, страница 4

154  Составить общее решение неоднородного уравнения в зависимости от правой части и корней характеристического уравнения:   

                    k₁=2, k₂=1, f(x)=e^2x                     y=C₁e^2x+C₂e^x+Ax·e^2x;

155  Составить общее решение неоднородного уравнения в зависимости от правой части и корней характеристического уравнения:

                    k₁=2=k₂, f(x)=e^2x           :             y=e^2x(C₁+C₂x)+Ax²·e^2x;

156  Составить общее решение неоднородного уравнения в зависимости от правой части и корней характеристического уравнения:

                   k₁₂=4±j, f(x)=e^4x              :          y=e^4x(Acosx+Bsinx)+Ae^4x;

157  Составить общее решение неоднородного уравнения в зависимости от правой части и корней характеристического уравнения:

                    k₁₂=2±j, f(x)=e^x               :          y=e^2x(Acosx+Bsinx)+Ae^x;

158  Составить общее решение неоднородного уравнения в зависимости от правой части и корней характеристического уравнения:

                     k₁=1, k₂=2, f(x)=e^x         :          y=C₁e^x+C₂e^2x+Ax·e^x;

159  Составить общее решение неоднородного уравнения в зависимости от правой части и корней характеристического уравнения:    

                     k₁=2, k₂=1, f(x)=x·e^x       :         y=C₁e^2x+C₂e^x+(Ax+B)e^x·x;

160  Составить общее решение неоднородного уравнения в зависимости от правой части и корней характеристического уравнения:

                     k₁=k₂=4, f(x)=4e^4x          :           y=e^4x(C₁+C₂x)+Ax²·e^4x;

             161  Изображение оригинала e^αt=f(t) равно: F(p)=;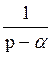

            162  Изображение оригинала e^4t=f(t) равно:   F(p)=;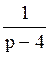

            163  Изображение оригинала e^–4t=f(t) равно:  F(p)=;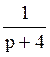

            164   Изображение оригинала e^–t=f(t) равно:      F(p)=;

            165   Изображение оригинала f(t)=t² равно:        F(p)=;

            166  Изображение оригинала f(t)=sin2t равно:  F(p)=.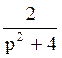

            167  Изображение оригинала f(t)=sin3t равно:   F(p)=;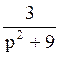

             168  Изображение оригинала f(t)=sint равно:    F(p)=;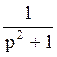

             169  Изображение оригинала f(t)=cost равно:    F(p)=;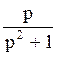

             170  Изображение оригинала f(t)=cos2t равно:  F(p)=;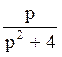

             171 Изображение оригинала f(t)=e^t·t² равно:F(p)=;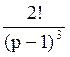

             172 Изображение оригинала f(t)=e^2t·t равно:F(p)=;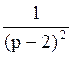

         173Изображение оригинала f(t)=e^2t·sin3t равно     

                        F(p)=;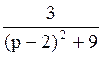

           174Изображение оригинала f(t)=e^3t·sin2t равно:

F(p)=;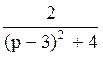

             175 Изображение оригинала f(t)=e^4t·sin3t равно:

F(p)=;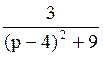

            176  Изображение оригинала f(t)=e^3t·cos2t равно:

F(p)=;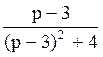

              177  Изображение оригинала f(t)=e^2t·cos3t равно:

F(p)=;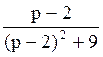

178  Изображение оригинала f(t)=t·sin2t равно:

F(p)=;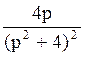

             179       Изображение оригинала f(t)=t·cos2t равно:

F(p)=;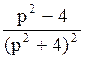

              180      Изображение оригинала f(t)=sh2t равно:

F(p)=;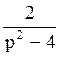

181 Составить оригинал по изображению  F(p)=:         f(t)=4;

            182  Составить оригинал по изображению  F(p)=:     f(t)=t²;

             183  Составить оригинал по изображению  F(p)=:       f(t)=t³;

              184  Составить оригинал по изображению  F(p)=:    f(t)=2e^8t;

              185  Составить оригинал по изображению  F(p)=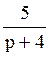:      f(t)=5e^–4t;

             186  Составить оригинал по изображению  F(p)=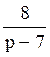:       f(t)=8e^–7t;

             187  Составить оригинал по изображению  F(p)=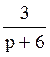:       f(t)=3e^–6t;

            188  Составить оригинал по изображению  F(p)=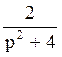:       f(t)=sin2t;

            189 Составить оригинал по изображению  F(p)=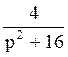:      f(t)=sin4t;

            190 Составить оригинал по изображению  F(p)=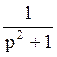:        f(t)=sint;

            191 Составить оригинал по изображению  F(p)=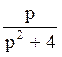:       f(t)=cos2t;

            192 Составить оригинал по изображению  F(p)=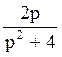:        f(t)=2cos2t;

           193Составить оригинал по изображению  F(p)=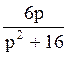:        f(t)=6cos4t;

          194Составить оригинал по изображению  F(p)=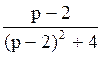:   f(t)=e^{2 t} · cos2t;

           195 Составить оригинал по изображению  F(p)=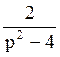:         f(t)=sh2t;

           196 Составить оригинал по изображению  F(p)=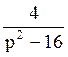:      f(t)=sh4t;

           197 Составить оригинал по изображению  F(p)=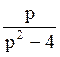:      f(t)=ch2t;

          198 Составить оригинал по изображению  F(p)=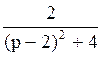:   f(t)=e^{2 t} · sin2t;

           199 Составить оригинал по изображению  F(p)=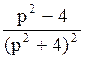:        f(t)=t·cos2t;

           200 Составить оригинал по изображению  F(p)=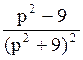:       f(t)=t·cos3t;