Неопределенный интеграл. Определенный интеграл. Подстановка к уравнению. Тип дифференциального уравнения, страница 2

4)  ∞.

                  80 Определенный интеграл 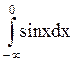  равен:   –∞.

           81   Указать подстановку к уравнению: y′+P(x)y=Q(x) :     y=uv;

           82  Указать подстановку к уравнению: y′cosx=(y+1)sinx:    разделить переменные.

           83  Указать подстановку к уравнению: φ₁(x)ψ₁(y)dx+φ₂(x)ψ₂(y)dy=0 :  разделить переменные;

           84   Указать подстановку к уравнению: φ₁(x)ψ₁(y)+φ₂(x)ψ₂(y)·y′=0 :    разделить переменные;

           85   Указать подстановку к уравнению: (1+x²)y′–2xy=(1+x²)² :      y=uv;

           86   Указать подстановку к уравнению: x²y′+y²–2xy =0:     y=ux;

           87   Указать подстановку к уравнению: F(x;y′;y″)=0:     y′=t;

           88   Указать подстановку к уравнению: F(y;y′;y″)=0:      y′=t;

           89   Указать подстановку к уравнению: y″+y′tgx=sin2x  :   y′=t;

           90   Указать подстановку к уравнению: y·y″–2(y′)²=0 :    y′=t;

           91   Указать подстановку к уравнению: (x²+2xy)dx+xydy=0 :    y=ux;

           92   Указать подстановку к уравнению: y′=+sin  :    y=ux;

           93    Указать подстановку к уравнению: =y–xy′  :    y=ux;

           94    Указать подстановку к уравнению: 2x²y′=y²+x²   :    y′=xu′+u;

           95    Указать подстановку к уравнению: xy′=y·(1+ℓn)   :       y′=xu′+u;

              96        Указать подстановку к уравнению: y′=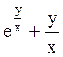      :      y′=u′x+u;

              97        Указать подстановку к уравнению: y′+2xy=2x²     :   y′=u′v+uv′;

              98        Указать подстановку к уравнению: y′+=x²         :     y′=u′v+uv′;

             99         Указать подстановку к уравнению: y′=x²+2x–2y     :      y′=u′v+uv′;

             100       Указать подстановку к уравнению: y′+2xy=x·sinx          :     y′=u′v+uv′;

             101        Определить тип дифференциального уравнения:     φ₁(x)ψ₁(y)dx+φ₂(x)ψ₂(y)dy=0  c разделяющимися переменными;

              102      Определить тип дифференциального уравнения:     φ₁(x)ψ₁(y)+φ₂(x)ψ₂(y)·y′=0  c разделяющимися переменными;

              103      Определить тип дифференциального уравнения:      y′cosx=(y+1)sinx                      c разделяющимися переменными;

              104      Определить тип дифференциального уравнения:      y′+P(x)y=Q(x)              линейное;

              105      Определить тип дифференциального уравнения:      (1+x²)y′–2xy=(1+x²)²            линейное;

              106      Определить тип дифференциального уравнения:       x²·y′+y²–2xy=0                    однородное І порядка;

              107      Определить тип дифференциального уравнения:       F(x;y′;y″)=0          линейное ІІ порядка;

              108      Определить тип дифференциального уравнения:       F(y;y′;y″)=0         с понижением порядка;

              109      Определить тип дифференциального уравнения:       y″+y′tgx=sin2x      с понижением порядка.

            110        Определить тип дифференциального уравнения:       y·y″–2(y′)²=0          с понижением порядка;

              111       Определить тип дифференциального уравнения:      y′+2xy=x·sinx

1)  линейное ІІ порядка;

2)  однородное І порядка;

              112      Определить тип дифференциального уравнения:        (x²+2x–2y)dx=dy         линейное;

              113      Определить тип дифференциального уравнения:        y′+=x²               линейное;

             114       Определить тип дифференциального уравнения:       y′+2xy=2x²   линейное;

              115      Определить тип дифференциального уравнения:        y″–=0           с понижением порядка;

             116       Определить тип дифференциального уравнения:       x³y″+x²y′=1         с понижением порядка;

              117      Определить тип дифференциального уравнения:        y″+y′tgx=sin2x    с понижением порядка;

              118      Определить тип дифференциального уравнения:         (x²+2xy)dx+xydy=0       однородное І порядка;

              119      Определить тип дифференциального уравнения:          y′=+sin            однородное І порядка;

             120       Определить тип дифференциального уравнения:         =y–xy′        однородное І порядка;

              121      Составить общее решение однородного уравнения:   y″–y′=0  :        y_o=C₁+C₂e^x;

              122      Составить общее решение однородного уравнения:   y″–y=0             y_o=C₁e^–x+C₂e^x;