Обработка векторов и матриц в среде Мathcad построение графиков функций одной переменной. Определение векторов и матриц в МС-документе

Определить вектор или матрицу явным образом - значит указать место в документе, записать нужное имя матрицы, команду присваивания и вставить шаблон матрицы. Затем шаблон заполняется числами.

Имя:= Шаблон

Вставить шаблон матрицы можно несколькими способами:

-Или выбрать в меню <Вставить>-<Матрица>

-Или нажать клавиши [Ctrl]+[M]

-Или щелкнуть по кнопке 1 палитры «Matrix»

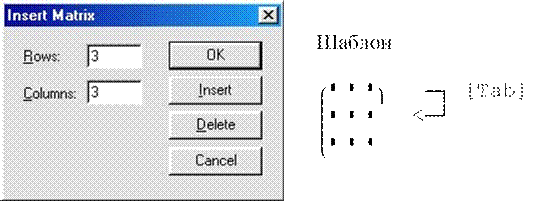
На экране появится окно диалога, в котором нужно указать количество строк (Rows) и столбцов (Columns). Для вектора Rows обозначает количество элементов, а Columns=1.

⎠

Переход к следующей ячейке выполняется при нажатии клавиши [Tab] или клавишами управления курсором. Пример определения вектора и матрицы:

⎛ 12 ⎞                     ⎛ 1 2 3 ⎞

Res := ⎜ 48                    W2a := ⎜ 4 5 6

⎜                         ⎜

⎝ −7 ⎠                    ⎝ 7 8 9 ⎠

Отдельный элемент вектора или матрицы обозначается нижним индексом. Переход в режим набора индекса:     или клавиша “[“,    или кнопка 2 палитры «Matrix».

Возврат в основной уровень - клавиша «Пробел». Для элемента матрицы указывают в индексе номер строки и номер столбца через запятую. (Например, нажатие клавиш M[1,2  дает в документе  M_1,2).

Отдельный элемент вектора или матрицы используется как обычная переменная: его значение можно вывести на экран, ему можно присвоить новое значение, его значение можно использовать в вычислениях. Например:

набрать на клавиатуре:	Res[1=     W2a[2,2=  z:Res[2+3*W2a[1,1  Z=
вид на экране:	Res     = 48          W2a       = 9          z:= Res   + 3W2a              z = 8 1                           2 2,                              2               1 1,

Неявный способ определения вектора или матрицы состоит в определении отдельного элемента. Как только определяется хотя бы один элемент нового вектора или матрицы, то его номер автоматически считается максимальным, и все предыдущие элементы считаются равными 0. Таким способом можно изменить размер и существующих матриц, например:

Fa2 := 20             Matr1 3, := 99                 ⎛⎜ ⁰0 ^⎞       Matr = ⎜ _{0 0 0      0} ⎞

⎛

Fa =

⎜                      ⎝ 0 0 0 99⎠

⎝ 20⎠

⎛ 1 2 3 0       0 ⎞

W2a2 4, := 50                 W2a = ^⎜ 4 5 6 0       0

⎜

⎝ 7 8 9 0 50⎠                              

Неявный способ можно использовать и для вычисления всех элементов, если задать выражение, в котором используется диапазонная переменная, логически соответствующая номеру элемента

k := 0 3..                                                          ⎛ 8 ⎞               ⎛ 1 ⎞

⎜                   ⎜

3                             ⎛ π ⎞                 ⎜ 27 ^⎟       _{W =} ⎜ 0.866⎟

V := (k + 2)             W := sin^⎜                 _{V =}

_{k                                k}          ⎝ _{k + 2} ⎠               ⎜ 64 ⎟            ⎜ 0.707⎟

⎜                   ⎜

⎝ 125⎠            ⎝ 0.588⎠

Зачастую бывает нужно вычислить вектор значений аргумента и вектор значений функции

fun(x) := x cos x⋅                  ( )                  a := 2 h := 0.1

j := 0 20..             x := a + h j⋅          y^j := fun x( )^j       x=       y= j

при этом имена вектора и функции должны быть различными.

После определения вектора или матрицы их можно обрабатывать как самостоятельные элементы, указывая только имя, или же изменять отдельные элементы (указывается индекс – номер элемента).

Используя определенные в документе векторы и матрицы, можно вычислять новые результаты, выполняя нужные команды палитры «Matrix», например:

⎛ 7 ⎞ ⎜ W1 :=      11 ⎜ ⎝ 19⎠	⎛ −2 ⎞ ⎜ W2 :=     8 ⎜ ⎝ 16 ⎠	⎛ 24 ⎞ ⎜ W1 × W2 =    −150 ⎜ ⎝ 78 ⎠
W1    = 23.043	W2   = 18	W1 W2⋅   = 378
⎛ −1 2 3 ⎞ ⎜ U :=      4     5 6 ⎜ ⎝ 7          8 9 ⎠	⎛ −1 4 7 ⎞ T ⎜ U = 2 5 8 ⎜ ⎝ 3          6 9 ⎠	⎛ 30 32 36 ⎞ 2 ⎜ U =     58    81     96 ⎜ ⎝ 88 126 150⎠
U = 6	⎛ 3 ⎞ 〈 〉2     ⎜ 6 U          = ⎜ ⎝ 9 ⎠	⎛ −0.5     1             −0.5 ⎞ − 1 ⎜ U      =      1       −5         3 ⎜ ⎝ −0.5 3.667 −2.167⎠

Примечания:

1)  Векторное произведение определено только для трехэлементных (трехмерных) векторов.

2)  При выводе на экран матриц большого размера отображается часть матрицы, причем остальные элементы можно просмотреть с помощью полос горизонтальной и вертикальной прокрутки.

3)  Для изменения начального номера элементов следует переопределить встроенную переменную ORIGIN. Например, для отсчета элементов от 1 определяют   ORIGIN:=1.

4)  Структуру вектора можно использовать для одновременного определения нескольких переменных.

⎛ a ⎞ ⎛ 12 ⎞ ⎛ x0 ⎞ ⎛ 1 ⎞ ⎛⎜ xn ⎞ := ⎜⎛ 0.2⋅xn 1− + yn 1− ⎞ ⎜ b := ⎜ 45 ⎜ := ⎜ n := 1 6..

⎜⎝ ^c ⎠ ⎜⎝ ⁻³ ⎠         ^⎜ y             ⎝ 2 ⎠     ^⎜_⎝ yn _⎠ ^⎜_⎝ xn 1−    + 0.1⋅yn 1− _{⎠ ⎝} 0 _⎠

Матричную структуру могут иметь и функции пользователя. 

⎛ x2 − 1 ⎞                       ⎛ 6.84 ⎞

α( )x := ⎜                       α(2.8) = ⎜

⎝ sin x( + 1) ⎠                    ⎝ −0.612⎠

⎛ p + s          p s⋅ ⎞                     ⎛ 8        15 ⎞

f p s( , ) := ⎜f 3 5( , ) = ⎜

                                                                  ⎝ p +    s   p − s ⎠                    ⎝ 3.968 −2 ⎠

Результат вычислений можно сохранять как самостоятельный вектор ⎛ 6.84 ⎞

res := α(2.8) res = ⎜ ⎝ −0.612⎠ или как вектор отдельных переменных ⎛ ta ⎞

⎜⎝ tb ⎠ := α(2.8)           ta = 6.84              tb = −0.612

Эти примеры отражают возможности Mathcad по созданию и обработке