Формулы конечно-разностной аппроксимации производных и численное исследование их точности для непрерывных функций

ЛАБОРАТОРНАЯ РАБОТА ПММ-2-2-06

ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ

КОНЕЧНО-РАЗНОСТНЫХ ПРОИЗВОДНЫХ

Цель работы: изучение формул конечно-разностной аппроксимации производных и численное исследование их точности для непрерывных функций.

ВОПРОСЫ ДЛЯ ПОДГОТОВКИ ПО КОНСПЕКТУ ЛЕКЦИЙ

1.  Разложение непрерывной функции в ряд Тейлора.

2.  Получение соотношений для первых конечно-разностных производных

3.  Вывод формулы для второй конечно-разностной производной.

4.  Оценка точности формул для конечно-разностных производных.

СОДЕРЖАНИЕ ЗАДАНИЯ

ЗАДАЧА 1.  Исследование первых конечно-разностных производных. Составить программный блок, в котором для функции f(x), начиная с точки x₀, с шагом h вычисляется:

-  значения аргумента x_i и функции f(x_i);

-  точное значение f '(x_i);

-  численное значение f ‘(x_i) по формуле с разностями вперед;

-  абсолютная погрешность вычисления f ‘(x_i)

Результаты в последней строке программного блока объединить в таблицу функцией augment.

Варианты функций – см. в Приложении.

Пример. Расчет первой конечно-разностной производной с шагом вперед

f(x) := exp x( )         d

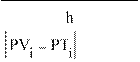f(x) → exp(x) f1(x) := exp x( )

PB x0 h(           ,            ,fun,fun1) :=         for i ∈ 0 10..

x ← x0+ i h⋅ i

PTi ← fun1 x( )_i

fun x( _i + h) − fun x( )_i

PV ← i

DV ←

i

augment x PT( , ,PV,DV)                   

W  := PB 1 0.1( , ,f,f1)

X  F'точн     F'вперед    Delta 

	0		1	2	3
0		1	2.7183	2.8588	0.1406
1		1.1	3.0042	3.1595	0.1553
2		1.2	3.3201	3.4918	0.1717
3		1.3	3.6693	3.859	0.1897
4		1.4	4.0552	4.2649	0.2097
5		1.5	4.4817	4.7134	0.2317
6		1.6	4.953	5.2091	0.2561
7		1.7	5.4739	5.757	0.2831
8		1.8	6.0496	6.3625	0.3128
9		1.9	6.6859	7.0316	0.3457
10		2	7.3891	7.7711	0.3821

W =

DVmax:= max W( 〈 〉³ )      DVmax= 0.3821                                            

Реализовать вызов программного блока для h=0.1 и h=0.05. 

Записать, во сколько раз уменьшилась максимальная погрешность результатов при уменьшении шага h сетки? Каков порядок сходимости конечноразностной производной?

ЗАДАЧА 2.  Выполнить те же действия для 

-  первой конечно-разностной производной с шагом назад

-  первой конечно-разностной производной центральной - второй конечно-разностной производной.

В каждом случае реализовать вызов программного блока для h=0.1 и h=0.05 и определить, во сколько раз уменьшилась максимальная погрешность результатов при уменьшении шага h сетки? Каков порядок сходимости второй конечноразностной производной?

Приложение. Варианты функций для исследования

1)  f(x)=exp(0.75x);  x₀=2;  ∆x=0.1

2)  f(x)=sin(x);      x₀=1;  ∆x=0.1

3)  f(x)=ln(x+1);     x₀=2;  ∆x=0.2

4)  f(x)=sin(x-2);    x₀=2;  ∆x=0.05

5)  f(x)=1/(x+2);     x₀=1;  ∆x=0.1

6)  f(x)=cos(x);      x₀=2;  ∆x=0.1

7)  f(x)=tg(x);       x₀=0; ∆x=0.1

8)  f(x)=x;          x₀=5;  ∆x=0.1

9)  f(x)=exp(0.28x);  x₀=2;  ∆x=0.1

10)  f(x)=cos(2x);   x₀=2; ∆x=0.1

11)  f(x)=1/x;       x₀=2;  ∆x=0.1

12)  f(x)=exp(-x);   x₀=0; ∆x=0.1

13)  f(x)=cos(x-1);  x₀=1;  ∆x=0.1

14)  f(x)=sin(x/2);  x₀=0;  ∆x=0.1

15)  f(x)=exp(x/2);  x₀=1;  ∆x=0.1

16)  f(x)=1/(x+1);   x₀=0;  ∆x=0.1

17)  f(x)=exp(0.5x);  x₀=2;  ∆x=0.1

18)  f(x)=sin(x-1);   x₀=1;  ∆x=0.1

19)  f(x)=ln(x+3);     x₀=2;  ∆x=0.2

20)  f(x)=sin(x-5);    x₀=2;  ∆x=0.05

21)  f(x)=1/(x+4);     x₀=1;  ∆x=0.1

22)  f(x)=cos(x+1);      x₀=2;  ∆x=0.1

23)  f(x)=tg(x);        x₀=0; ∆x=0.1

24)  f(x)= x+1;         x₀=5;  ∆x=0.1

25)  f(x)=exp(0.8x);    x₀=2;  ∆x=0.1

26)  f(x)=cos(0.5x);    x₀=2; ∆x=0.1

27)  f(x)=1/(x+4);      x₀=2;  ∆x=0.1 28) f(x)=exp(x+1);     x₀=0; ∆x=0.1

29) f(x)=cos(x-3);     x₀=1;  ∆x=0.1 30) f(x)=sin(x/3);     x₀=0;  ∆x=0.1

Составил:   2009-2012  v2.4