Программно-методологические вопросы статистического наблюдения в соответствии с выданным заданием, страница 6

а) базисный темп роста:

Тр_бi = y_i  : y_oi.                                                                                                   (19)

В нашем примере:

Тр_б1 = 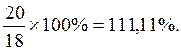          Тр_б2 =

б) базисный темп  прироста:

Тп_i (%) = Тр_i (%) – 100.                                                                                (20)

В нашем примере:

Тп₁ = 111,11 - 100 = 11,11%.              Тп₂ = 100 – 100 = 0.

3.  Рассчитаем средние показатели динамики.

Выделяют следующие средние показатели динамики:

а) средний уровень ряда:

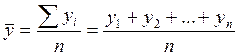.                                                                              (21)

В нашем случае:

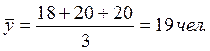
б) средний абсолютный прирост:

.                                                                                                (22)

В нашем случае:

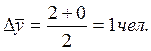
в) средний темп роста:

.                                                                                      (23)

В нашем примере:

г) средний темп прироста:

.                                                                                                      (24)             В нашем случае:

                       

4.  Выявим основную тенденцию развития.

Выявление основной тенденции развития по показателю «средняя списочная численность» будем проводить на основе данных таблицы 7, используя метод аналитического выравнивания.

Для выравнивания ряда динамики по прямой используем уравнение:

                                                                                                  (25)

Применяя способ наименьших квадратов для нахождения параметров уравнения, необходимо преобразовать исходный ряд динамики (табл. 6) таким образом, чтобы  сумма значений показателей времени t была равна 0 (табл. 8).

Таблица 8

Условное обозначение времени t

Год	1-й	2-й	3-й
t	-1	0	1

Тогда путем преобразований получаем формулы для нахождения параметров уравнения:

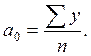                                                                                                                             (26)

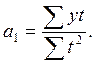                                                                                                       (27)

В нашем примере:

.                                                             

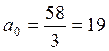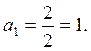
Получаем следующее уравнение:

Подставляя в полученное уравнение значения t, получим выровненные уровни ряда динамики. В результате выявим основную тенденцию развития.

5. Проведем статистическое изучение сезонных колебаний.

Индексы сезонности определим на основе данных таблицы 1 по показателю «средняя списочная численность персонала». Все расчеты сведем в таблицу 9.

Таблица 9

Расчет индексов сезонности

№ магазина	Средняя списочная численность, чел.			В среднем за три гола	Индекс сезонности
	1-й год	2-й год	3-й год
1	12	14	14	13	68,42
2	15	17	17	16	84,21
3	16	18	18	17	89,47
4	21	23	23	22	115,79
5	22	24	24	23	121,05
6	22	24	24	23	121,05
7	18	21	21	20	105,26
8	19	22	22	21	110,53
9	15	17	17	16	84,21
10	22	21	21	21	110,53
Средний уровень ряда	18	20	20	19	100

Расчеты по показателю «прибыль» проводятся аналогично.

На основе данных таблицы 9 построим сезонную волну показателя «средняя списочная численность».

Рис. 3.  - Сезонная волна показателя «средняя списочная численность»

Выводы после каждой лабораторной работы формулируются студентами самостоятельно.