Программно-методологические вопросы статистического наблюдения в соответствии с выданным заданием, страница 4

а) относительный показатель динамики

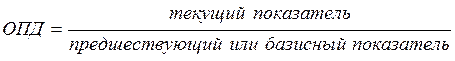.                     (3)

Расчёты проведем в табличной форме (табл. 5).

Таблица 5

Расчёт показателей динамики

№ магазина	Показатель динамики
	с постоянной базой сравнения		с переменной базой сравнения
	2-й год/ 1-й год	3-й год/1-й год	2-й год/ 1-й год	3-й год/2-й год
1	14 : 12 = 1,17	14 : 12 = 1,17	14 : 12 = 1,17	14 : 14 = 1
2	17 : 15 = 1,13	17 : 15 = 1,13	17 : 15 = 1,13	17 : 17 = 1
3	18 : 16 = 1,125	18 : 16 = 1,125	18 : 16 = 1,125	18 : 18 = 1
4	23 : 21 =  1,09	23 : 21 =  1,09	23 : 21 =  1,09	23 : 23 = 1
5	24 : 22 = 1,09	24 : 22 = 1,09	24 : 22 = 1,09	24 : 24 = 1
6	24 : 22 = 1,09	24 : 22 = 1,09	24 : 22 = 1,09	24 : 24 = 1
7	21 : 18 = 1,17	21 : 18 = 1,17	21 : 18 = 1,17	21 : 21 = 1
8	22 : 19 = 1,16	22 : 19 = 1,16	22 : 19 = 1,16	22 : 22 = 1
9	17 : 15 = 1,13	17 : 15 = 1,13	17 : 15 = 1,13	17 : 17 = 1
10	21 : 22 = 0,95	21 : 22 = 0,95	21 : 22 = 0,95	21 : 21 = 1

б) относительный показатель структуры

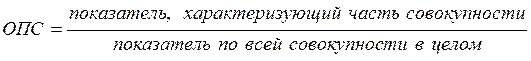.(4)

Расчёт относительных показателей структуры представлен в структурной группировке средней списочной численности.

в) относительный показатель сравнения

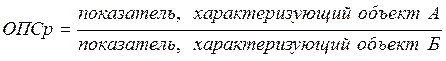.                                              (5)

Произведем сравнение показателей за 3-й год. В качестве базы сравнения возьмем наибольший показатель. В нашем случае это средняя списочная численность в 5 и 6 магазинах.

                                          

                                

                                                       

                                                  

                                                        

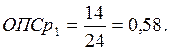
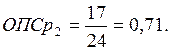
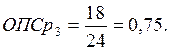
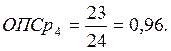
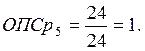
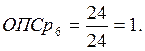
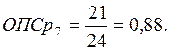
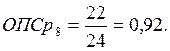
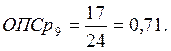
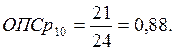
Расчеты за другие годы и по показателю «прибыль» проводятся аналогично.

2. Рассчитаем степенные средние показатели.

Расчёты произведем на основе данных типологической группировки по группировочному признаку за 1-й год.

В нашем случае применим формулу  средней арифметической взвешенной:

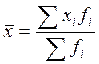.     (6)

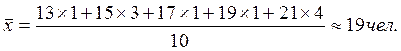
За 2-й, 3-й годы расчеты проводятся аналогично.

3. Определим структурные средние показатели.

Расчеты произведем на основе данных типологической группировки по группировочному признаку за 1-й год.

В интервальных рядах мода и медиана определяются по следующим формулам:

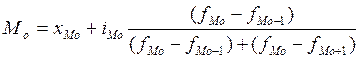.                                         (7)

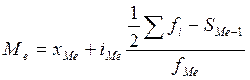.(8)

В нашем примере:

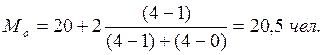
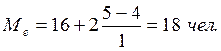
За 2-й, 3-й годы расчеты проводятся аналогично.

Лабораторная работа 4 (2 часа)

Цель лабораторной работы: осуществить расчёт показателей вариации.

Порядок выполнения работы:

1.  рассчитать абсолютные и средние показатели вариации;

2.  определить показатели относительного рассеивания;

3.  сформулировать выводы.

1.  Рассчитаем абсолютные и средние показатели вариации.

Расчёты произведем на основе данных типологической группировки по группировочному признаку за 1-й год.

Абсолютный показатель вариации – размах вариации, который определяется по формуле:

R = x_max - x_min                                                                                                   (9)

R = 22-12 = 10 чел.

Выделяют следующие средние показатели вариации:

а) среднее линейное отклонение

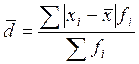.(10)

В нашем случае:

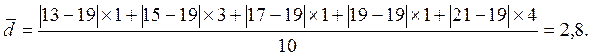
б) дисперсия

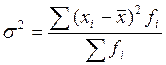.               (11)

В нашем примере:

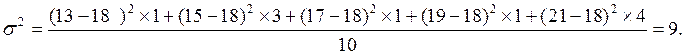
в) среднее квадратическое отклонение:

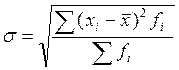.                                                                                         (12)

В нашем примере:

2.  Определим показатели относительного рассеивания.

а) коэффициент осцилляции:

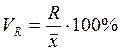.                                                                                                  (13)

В нашем случае:

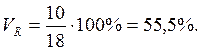
б) линейный коэффициент вариации: