Методы анализа электрических цепей. Расчет токов и напряжений в линейной электрической цепи по методу узловых напряжений и методу контурных токов

Федеральное агентство по образованию Российской Федерации

ГОУ ВПО Дальневосточный государственный технический университет

(ДВПИ имени Куйбышева)

Кафедра теоретической и общей электротехники

Методы анализа электрических цепей

Часть II

Расчет токов и напряжений в линейной электрической цепи по методу узловых напряжений и методу контурных токов

Расчетно-пояснительная записка к курсовой работе по теоретическим основам электротехники

Выполнил студент группы Р-4011

Проверил преподаватель

Владивосток, 2008 г.

Содержание

Содержание............................................................................................ 2

Введение................................................................................................. 3

Задание на курсовую работу................................................................. 4

1 Анализ сложных (разветвленных) электрических цепей................. 5

1.1 Построение схемы разветвленной электрической цепи............. 5

1.2 Анализ схемы методом узловых напряжений............................. 6

1.3 Анализ схемы методом контурных токов................................... 8

1.4 Проверка баланса активных и реактивных мощностей рассчитываемой ................................................................................... электрической цепи.......................................................................... 11

1.5 Векторно-топографические диаграммы.................................... 12

 

Введение

Целью выполнения курсовой работы по разделу «Анализ линейных электрических цепей в установившемся режиме» дисциплины «теоретические основы электротехники» является:

-  закрепление теоретических знаний но этому разделу и самостоятельное применение их к анализу простейших и сложных электрических цепей;

-  выработка навыков и умений в выполнении типового анализа цепей, знакомство с правилами оформления технической документации в соответствии с действующими стандартами.

В данной работе мною рассмотрены и описаны основные принципы анализа линейных электрических цепей в установившемся синусоидальном режиме. Сама курсовая работа состоит из двух основных частей: 1) анализ простейшей электрической цепи;

2) анализ сложной электрической цепи;

В первой части мною был проведен анализ простейшей электрической цепи под воздействием синусоидального ЭДС, т. е. цепи, содержащей лишь один источник ЭДС и лишь последовательное и параллельное соединение элементов. Этот анализ осуществляется на основе комплексного метода, который можно применять только в случае, когда сигнал синусоидальный, а также на основе первого и второго законов Кирхгофа в комплексной форме.

Задание на курсовую работу

Анализ сложных (разветвленных) электрических целей.

1.  Построить схему разветвленной цепи, используя кодировку ветвей в соответствии с вариантом.

2.  Определить напряжения и токи ветвей по методу узловых напряжений.

3.  То - же методом контурных токов. Независимые контуры выбрать в соответствии с заданными хордами.

4.  Проверить правильность решения на основании баланса мощностей цепи.

5.  Для заданной схемы построить топографическую диаграмму напряжений, совмещенную с векторной диаграммой токов.

1  Анализ сложных (разветвленных) электрических цепей

1.1  Построение схемы разветвленной электрической цепи

Построим схему для варианта №12, в котором участки цепи представлены кодами:

Участок Э. Ц.	Z1	Z2	Z3	Z4	Z5	Z6
	1	3	9	1	5	1

Граф расчетной схемы приведен на рис. 1.

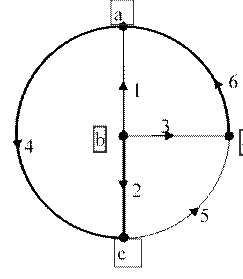
Рисунок 1. Граф сложной электрической цепи

a

d(БУ )

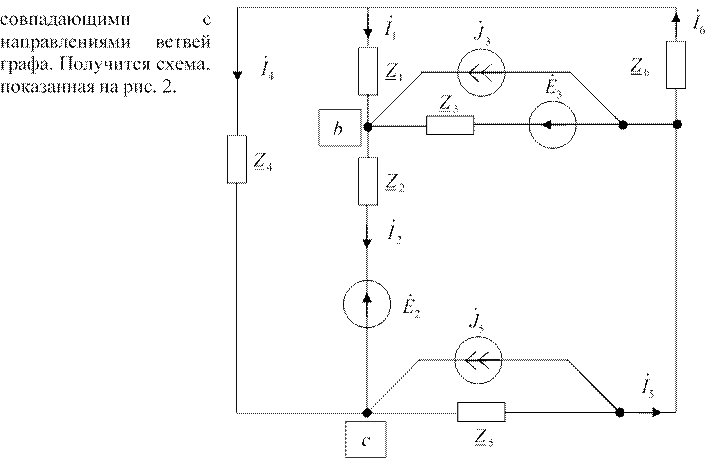Воспользовавшись видом графа, заменим каждую его ветвь соответствующей заданному коду схемой замещения. При этом, условно положительные направления тока в каждой из ветвей выбираем

Рисунок 2 Схема построения сложной электрической цепи

Параметры пассивных элементов, источников ЭДС и тока:

Z1 =1 30∠  0 Ом	E&1m =10∠00 В	J&1m =1 0∠ 0 А
Z2 = 2∠00 Ом	E&2m =12∠450 В	J&2m = 2∠300 А
Z3 = 4∠900 Ом	E&3m =14 180∠ 0 В	J&3m = 3∠−300 А
Z4 = 3 0∠ 0 Ом	E&4m =16 90∠ 0 В	J&4m = 4∠2700 А
Z5 = 6∠900 Ом	E&5m =18∠− 450 В	J&5m = 5∠600 А
Z6 = 5∠−900 Ом	E&1m = 20∠−900 В	J&1m = 6 90∠    0 А

Определим действующие значения источников ЭДС и тока в схеме:

E&₂ = E&_2m /       2 = + =6            j6     8.485∠45⁰ В

E&₃ = E&_3m /      2 =−9.899 = 9.899∠−180⁰ В

J&₃ = J&_3m /      2 =1.837 − j1.061= 2.121∠−30⁰ А

J&₅ = J&_5m /       2 =1.768− j3.062 = 3.536∠−60⁰ А

1.2  Анализ схемы методом узловых напряжений

Представим электрическую цепь в виде, удобном для анализа методом узловых напряжений (рис. 3). 

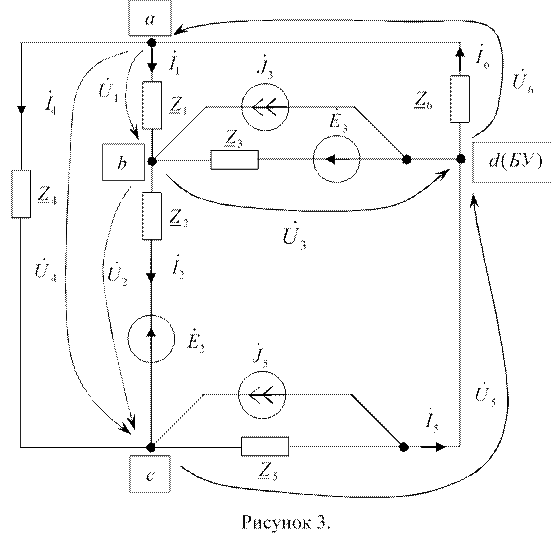
Для составления системы линейных уравнений по методу узловых напряжений рассчитаем проводимости ветвей.

См

См

См

См

См

См

Преобразуем во второй и третьей ветвях источники ЭДС в эквивалентные источники тока: J&₂ = E&₂ ⋅Y₂

J&3 = E&3 ⋅Y3

Составим систему линейных алгебраических уравнений с комплексными коэффициентами по методу узловых напряжений. Число уравнений – 3, их общий вид следующий:

Yaa ⋅U&a +Yab ⋅U&b +Yac ⋅U&c = J&a 

Y_ba ⋅U&_a +Y_bb ⋅U&_b +Y_bc ⋅U&_c = J&_b , 

                                                                 ^        &           &          &     &

Yca ⋅Ua +Ycb ⋅Ub +Ycc ⋅Uc = Jc

Y _aa = Y₁ +Y₄ +Y₆ Y_ab = Y_ba = −Y₁ = −0.866+ j0.5 =1∠−30⁰ где ^Y _bb = Y₁ +Y₂ +Y₃ , ^Y _ac = Y_ca = −Y₄ = −0.333 = 0.333 180∠ ⁰ ,