Методы анализа электрических цепей. Расчет токов и напряжений в линейной электрической цепи по методу узловых напряжений и методу контурных токов, страница 2

                                      ^Y _cc = Y₂ +Y₄ +Y₅ ^Y_bc = Y_cb = −Y₂ = −0.5 = 0.5 180∠       ⁰

J&_a = 0

 &_b = E&₂ ⋅Y₂ + E&₃ ⋅Y₃ + J&₃ = 4.837+ j4.414 = 6.548∠42⁰  J

^ J&_c = −E&₂ ⋅Y₂ + J&₅ = −1.232+ j0.062 =1.234∠−3⁰

Решая систему, находим узловые напряжения:

U&_a = −13.949+ j23.223 = 27.09∠−59⁰

^U&_b = −15.688+ j21.022 = 26.23∠−53⁰   

^U&_c = −20.064+ j17.964 = 26.931∠− 42⁰

По найденным узловым напряжениям найдем напряжения в ветвях:

U&₁ =U&_a −U&_b =1.739+ j2.201= 2.805 52∠ ⁰

U&₂ =U&_b −U_c − E&₂ = −1.624− j2.942 = 3.36∠61⁰

U&₃ =U&_b − E&₃ = −5.788+ j21.022 = 21.804∠−75⁰

U&₄ =U&_a −U&_c = 6.115+ j5.259 = 8.065∠41⁰                 

U&₅ =U&_c = −20.064+ j17.964 = 26.931∠− 42⁰

U&₆ = −U&_a =13.949− j23.223 = 27.09∠−59⁰

Определим токи ветвей:

I&₁ =U&₁⋅Y₁ = 2.606+ j1.037 = 2.805∠22⁰ ,    A

I&₂ =U&₂ ⋅Y₂ = −0.812− j1.47 =1.679∠61⁰ ,    A

I&₃ =U&₃⋅Y₃ − J&₃ =3.418+ j2.508= 4.239∠36⁰ ,     A

I&₄ =U&₄ ⋅Y₄ = 2.038+ j1.753= 2.688∠41⁰ ,     A      

I&₅ =U&₅ ⋅Y₅ − J&₅ =1.226+ j0.282 =1.258 13∠ ⁰ ,   A

I&₆ =U&₆ ⋅Y₆ = 4.645+ j2.79 =5.418 31∠ ⁰ ,    A

1.3  Анализ схемы методом контурных токов

d(БУ )

Построим схему для исследования ее методом контурных токов (рис. 4):

Рисунок 4 Схема сложной электрической цепи

В соответствии с заданным пересечением ветвей дерева (2,4,6) строим граф схемы

(рис. 5). 

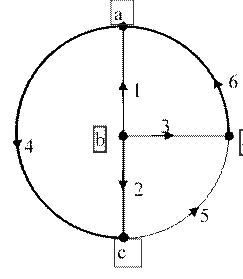
Рисунок 5 Граф расчетной схемы.

Выбор системы независимых контуров (контурных токов) осуществим с помощью дерева графа. В нашем случае ветви дерева – 2, 4, 6. Каждому дереву соответствуют связи (хорды) – ветви графа, дополняющие дерево до полного множества его ветвей (1, 3, 5). Основные контуры – контуры, в которые входит одна лишь хорда, остальные – ветви дерева.

Обозначим токи этих контуров как ^{I I I}& & &_{x y z} . Условные положительные направления контурных токов выбраны в соответствии с направлениями их связей. Уравнения имеют следующий вид:

Z xx ⋅I&x + Z xy ⋅I&y + Z xz ⋅I&z = E&xx

Z yx ⋅I&x + Z yy ⋅I&y + Z yz ⋅I&z = E&yy ,

Z zx ⋅I&x + Z zy ⋅I&y + Z zz ⋅I&z = E&

                                                                                                          zz

где собственные сопротивления контуров Z _xx , Z _yy , Z _zz являются суммой комплексных сопротивлений ветвей, входящих в соответствующие контуры; общие сопротивления контуров Z_xy = Z _yx , и т. д. равны сумме комплексных сопротивлений ветвей, общих для соответствующих, причем берется со знаком плюс (минус), если направления соответствующих контурных токов в общих ветвях совпадают (не совпадают); контурные ЭДС E&_xx , ^E&_yy , E&_zz определяются суммой ЭДС всех входящих в контур источников, взятых со знаками плюс (минус), если направление совпадает (не совпадает) с направлением контурного тока; токи I&_xx , ^I&_yy , I&_zz являются искомыми величинами.