Численные методы линейной алгебры. Численные методы решения СЛАУ. Метод Гаусса. Метод прогонки

1. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ

В разделе «Численные методы линейной алгебры» рассматриваются численные методы решения систем линейных алгебраических уравнений (СЛАУ)  и численные методы решения задач на собственные значения и собственные векторы матриц.

Среди численных методов алгебры существуют прямые методы, в которых решение получается за конечное фиксированное число операций и итерационные методы, в которых результат достигается в процессе последовательных приближений.

1.1. Численные методы решения СЛАУ

Из прямых методов решения СЛАУ рассмотрим методы Гаусса и прогонки.

1.1.1. Метод Гаусса

В методе Гаусса матрица СЛАУ с помощью равносильных преобразований  преобразуется в верхнюю треугольную матрицу, получающуюся в результате прямого хода. В обратном ходе определяются неизвестные. 

Пусть дана СЛАУ

a11x1 + a12x2 +...+ a1n xn = b1 a21x1 + a22x2 +...+ a2n xn = b2



................................

an1x1 + an2x2 +...+ ann xn = bn

Запишем расширенную матрицу системы:

                                                         x1         x2                x3 L xn             b

Ведущаястрока →     a11       a12             a13 L a1n        b1 (− a21a11);(− a31a11);K;(− an1a11)

                                                 a21       a22             a23 L a2n             b2 

                                              a31       a32             a33 L a3n           b3         1−й шаг→        

 L L L L L L 

                                              an1       an2             an3 L ann           bn 

↑ Ведущийстолбец

На первом шаге алгоритма Гаусса выберем диагональный элемент a₁₁ ≠ 0(если он равен 0, то первую строку переставляем с какой-либо нижележащей строкой) и объявляем его ведущим, а соответствующую строку и столбец, на пересечении которых он стоит - ведущими. Обнулим элементы a₂₁,...,a_n1 ведущего столбца. Для этого сформируем числа (− a₂₁a₁₁);(− a₃₁a₁₁);...;(− a_n1a₁₁). Умножая ведущую строку на число (− a₂₁a₁₁), складывая со второй и ставя результат на место второй строки, получим вместо элемента

a₂₁ нуль, а вместо элементов a_{2 j,} j = 2,n , b₂  – соответственно элементы a¹_{2 j} = a_{2 j} + a_1j (− a₂₁ a₁₁), j = 2,n , b₂¹ = b₂ + b₁(− a₂₁a₁₁) и т.д. Умножая ведущую строку на число (− a_n1 a₁₁), складывая с n-ой строкой и ставя результат на место n-ой строки, получим вместо элемента a_n1 нуль, а остальные элементы этой строки будут иметь вид: a¹_nj = a_nj + a_1j (− a_n1a₁₁), b_n¹ = b_n + b₁(− a_n1a₁₁). Сохраняя ведущую строку неизменной, получим в результате 1-го шага алгоритма Гаусса следующую матрицу:

                                                      x1         x2                x3 L xn             b

                                                         n2           n3                       nn           n 

↑ Ведущийстолбец

На втором шаге алгоритма Гаусса в качестве ведущего элемента выбирается элемент a₂₂¹ ≠ 0 (если он равен нулю, то вторую строку взаимно меняем на нижележащую строку).

Формируются числа ^_− a^a321^{1 }_;...;^_− ^aa¹ⁿ₁₂₂² _^_ , которые ставятся около ведущей строки. _{22 }

Умножая ведущую строку на число ^_− a^a₁³²¹₂₂ ^_ и складывая результат с третьей строкой, _

получим вместо элемента a₃₂¹ нуль, а вместо элементов a₃¹ _j , j = 3,n, b₃¹, Σ¹₃ – элементы

a32j = a31 j + a12 j − aa132122 ,         j = 3,n, b32 = b31 + b21− aa132122  ,. И так далее. Умножая ведущую 

строку на число ^− ^aa¹ⁿ₁₂₂² ^ , складывая результат с n-ой строкой и ставя полученную сумму 

на место n-ой строки, получим вместо элемента a¹_n2 нуль, а вместо элементов a¹_nj , b_n¹ , Σ¹_n - элементы anj2 = a1nj + a12j− aa1n1222 ,           j = 3,n, bn2 = bn1 + b21− aa1n1222  . Сохраняя 1-ую и 2-ую строки матрицы неизменными, получим в результате второго шага алгоритма Гаусса следующую матрицу: 

                                                        x1         x2                x3 L xn             b

a11 0	a12 a122	a13 a123	L an1               b1 L a12n           b21
0	0	a332	L a32n           b32
L 0	L 0	L a2	L L L L a2                 b2







Ведущаястрока →                                    3−й шаг→L (n−1)−й шаг→



                                                                 n3                       nn         n 

↑ Ведущийстолбец

После (n-1)-го шага алгоритма Гаусса получаем следующую расширенную матрицу, содержащую верхнюю треугольную матрицу СЛАУ:

                      x₁       x₂             x₃ L  x_n              b                                     

                  a11      a12             a13 L a1n                b1              



                 00 a0122 aa133232 LL aa1322nn            bb3212                             

                                                                 

L L L L L L L

                  0     0         0 L annn−1         bnn−1         

Прямой ход алгоритма Гаусса завершен.

В обратном ходе алгоритма Гаусса из последнего уравнения сразу определяется x _n , из предпоследнего - x _n−₁ и т.д. Из первого уравнения определяется x₁.

a_nnⁿ⁻¹x_n = b_nⁿ⁻¹                             ⇒ x _n

an−2 xn−1 + ann−−12nx n = bnn−−12        ⇒ x n−1  n− −1n 1

...................................

         ^a x_{11 1}+...+a x_{1n n} = b₁                  ⇒ x₁

Замечание 1. Если элементы какой-либо строки матрицы системы в результате преобразований стали равными нулю, а правая часть не равна нулю, то СЛАУ несовместна, поскольку не выполняются условия теоремы Кронекера-Капелли.

Замечание 2. Если элементы какой-либо строки матрицы системы и правая часть в результате преобразований стали равными нулю, то СЛАУ совместна, но имеет бесконечное множество решений, получающееся с помощью метода Гаусса для СЛАУ порядка r , где r - ранг матрицы исходной СЛАУ. 

Замечание 3. В результате прямого хода метода Гаусса можно вычислить определитель матрицы A исходной СЛАУ: 

det A = (−1) p a11a122a332 ⋅...⋅annn−1

При этом с помощью множителя (−1) ^p , где p - число перестановок строк в процессе прямого хода,  учитываются соответствующие перемены знаков вследствие перестановок строк. 

Замечание 4. Метод Гаусса можно применить для обращения невырожденной (det A ≠ 0) матрицы. 

Действительно, пусть требуется обратить невырожденную матрицу A = [a_ij ], i, j =1,n . Тогда, сделав обозначение A⁻¹ = X , X = [x_ij ], i, j =1,n , можно выписать

1 0 матричное уравнение AX = E , где E - единичная матрица E = ...  0 которого можно записать цепочку СЛАУ                  x11  1      x12   0        x1n   0 

0 1 ... 0

... ... ... ...

0 0 , на основе ... 1

A^⋅^xx...²¹n1 ^ ^{= }...⁰0^,       A^⋅^x^x..._n²²₂ ^ = ^...¹0^,        … A^⋅^xxnn ^   ^...1^0 ,  

каждую из которых можно решить методом Гаусса. При этом, поскольку верхняя треугольная матрица для всех этих СЛАУ будет одной и то же, то метод Гаусса применяется один раз. Строится следующая расширенная матрица:

x1n x2n ... xnn ... ... ... ...

             x12        x22       ...    xn2

             x11        x21       ...    xn1 b1        b2        .    bn

a₁₁               a₁₂            ...         a_1n   1          0          ...         0 a₂₁               a₂₂            ...         a_2n   0          1          ...         0

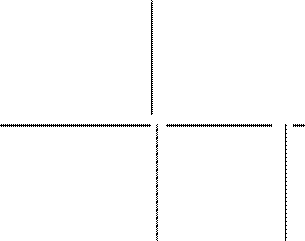... ... ... ... ... ... ... ... ... a_n1 a_n2 ... a_nn 0 0 ... 1

        В результате применения (n −1)-го шага метода Гаусса получаем:

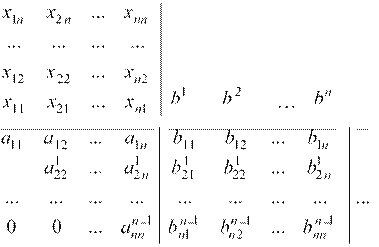
При этом первый столбец (x₁₁ x₂₁ ... x_n1)^T обратной матрицы определяется в обратном ходе метода Гаусса