Решение СЛАУ методом прогонки, простой итерации, методом Гаусса (исключения). Сплайн интерполяция, параболическая интерполяция, интерполяционный полином Лагранжа

Кафедра «Информационных технологий»

ЗАДАНИЕ

Студенту группы          1132                                   А.

^{(шифр группы)                                                       (Ф.И.О.)}

1. Тема проекта: Использование информационных технологий для решения прикладных задач таких как решения СЛАУ итерационным методом (простой итерации), методом прогонки и метода исключения Гаусса; нахождения недостающих значений функции (интерполирования) с помощью и. полинома Лагранжа, сплайна, параболической интерполяции.

2. Исходные данные к проекту:

1) дана СЛАУ

2)  даны значения нек-рой функции (даны точки Xi, значения берутся из задания №1

3. Содержание пояснительной  записки: Пояснительная записка включает в себя задание на выполнение работы, титульный лист, аннотацию, оглавление, введение, собственно текст пояснительной записки, выводы, библиографический список.

4. Перечень графического материала: Представление результатов в виде графиков.

Дата выдачи задания: 25.08.2005

Аннотация.

Пояснительная записка представляет собой отчет о выполнении курсовой работы. В ней рассматриваются вопросы нахождения неизвестных аргументов СЛАУ вышеуказанными методами и интерполяции. Расчеты проведены средствами пакета Microsoft Excel.

ЗАДАНИЕ. 2

Аннотация. 3

1. Постановка задачи. 5

Теоретическим минимум. 5

2.1 Метод прогонки: 5

2.2 Метод простой итерации. 6

2.3 Решение системы линейных алгебраических уравнений методом исключения Гаусса. 7

2.4 Интерполяционная формула Лагранжа. 7

2.5 Параболическая интерполяция. 9

2.6 Сплайн-интерполяция. 9

3. Расчеты в Microsoft Excel. 12

3.1   Решение СЛАУ методом простой итерации. 12

3.2   Решение СЛАУ методом прогонки. (СЛАУ таже) 13

3.3   Решение СЛАУ методом исключения Гаусса. (СЛАУ таже) 13

3.4 Интерполирование с помощью полинома Лагранжа. 14

3.5 Параболическое интерполирование. 14

3.6 Интерполирование сплайном.. 15

4. Построение графиков в Excel 17

Результаты интерполирования: 17

4.1 Приложение. 17

Заключение. 26

Список литературы. 27

 1. Постановка задачи.

Y1	Y2	Y3	F
10	4	0	13
2	10	5	14
0	2	10	15

1. Найти решение СЛАУ методом прогонки, простой итерации, методом Гаусса (исключения)

X	0	2	4
Y	Y1	Y2	Y3

2. Проинтерполировать найденные значения с помощью сплайна, параболической интерполяции, и по Лагранжу с шагом 0,01. Результаты представить на одном графике.

Теоретическим минимум.

2.1 Метод прогонки:

Метод прогонки состоит из прямой прогонки, т.е. нахождения промежуточных коэффициентов αk, βk, k=1,2,...n-1 по формулам:

;    k=1,…,n-1                                                 (1)

 -обратный ход прогонки;                 

k-1= αk-1k+ βk-1                                                                                   (2)

Подставим в выражение (1) вместо k-1 выражение (2), получим уравнение:

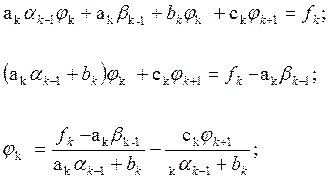
Прямой ход прогонки:

 

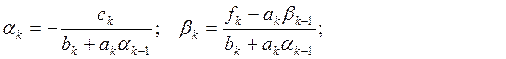
Пусть А – трёхдиагональная матрица, которую мы представим в виде

2.2 Метод простой итерации.

Приведем решаемую систему Ax=b эквивалентным преобразованием к виду:

x = C x + d

(1.11)

Это возможно сделать многими способами. Например, умножим слева обе части равенства 0 = -A x + b на произвольную невырожденную матрицу H и прибавим вектор x к правой и левой части полученного равенства:

x = x - H A x + H b = (E - H A) x + H b

Отсюда находим:

C º E - HA, d º Hb.

(1.12)

Матрицу H нужно выбирать так, чтобы C обладала определенными свойствами, о которых будет сказано ниже (теорема 1.1).

Итерационный процесс (то есть процесс последовательных приближений) метода простой итерации описывается формулой:

x(k+1) = C x(k) + d, k = 0, 1, ...,

(1.13)

где x⁽⁰⁾ - некоторое начальное приближение к решению (обычно полагают x⁽⁰⁾=d).

В координатной форме метод простой итерации записывается следующим образом:

x₁^(k+1) = c₁₁x₁^(k) + c₁₂x₂^(k) + ... + c_1nx_n^(k) + d₁ x₂^(k+1) = c₂₁x₁^(k) + c₂₂x₂^(k) + ... + c_2nx_n^(k) + d₂ ... x_n^(k+1) = c_n1x₁^(k) + c_n2x₂^(k) + ... + c_nnx_n^(k) + d_n

Таким образом i-тая компонента (k+1)-го приближения к решению вычисляется по формуле

(1.14)

2.3 Решение системы линейных алгебраических уравнений методом исключения Гаусса

  Рассматривается линейная система Ax = b, где A = ||a_ij|| - матрица системы, x = ||x_i|| - вектор-столбец неизвестных, b = ||b_i|| - вектор-столбец правых частей. Полагаем матрицу A невырожденной. Если A - вырожденная, то это обнаружится в процессе вычислений. Гауссово исключение состоит из двух этапов: прямого хода и обратной подстановки. Прямой ход заключается в преобразовании матрицы системы к верхнему треугольному виду:

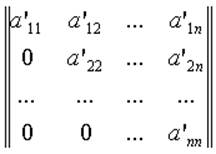
  Обратный ход заключается в решении системы с треугольной матрицей последовательным вычислением сначала x_n из последнего уравнения, затем x_n-1 - из предпоследнего, и т.д. до x₁. Коэффициенты матрицы системы и правые части редко бывают известны точно. Ошибки округлений, совершенные в процессе вычислений почти всегда