Решение дифференциальных уравнений в mathcad
Стандартная форма дифференциальных
уравнений 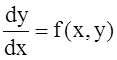
Уравнения высших порядков сводятся к уравнению первого порядка. Например:
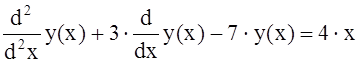 , где
, где 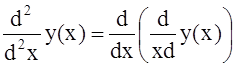
Вводятся новые функции:
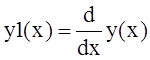 ,
, ![]()
Получается система уравнений в стандартной форме:
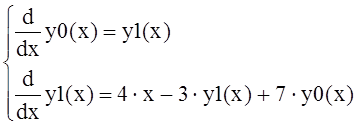
Тогда вектор производных 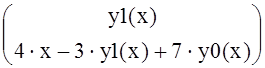
Для решения обыкновенных дифференциальных уравнений в mathcad используется функция odesolve в блоке given.
Пример.
 |
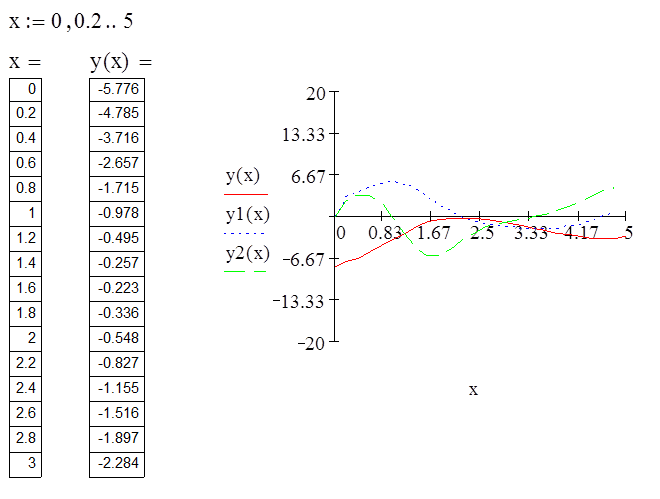
Формат вызова функции:
odesolve (x, xk, n)
x – переменная, по которой ведётся диффеенцирование;
xk – верхняя граница интервала, на котором ищется решение;
n – необязательный параметр – количество точек, на которое разбивается интеграл для численного поиска решения; если не задан, то подбирается;
Нижняя граница интервала, на котором ищется решение, берётся из начальных условий.
С помощью функции odesolve решаются уравнения высших порядков. Тогда в начальные условия добавляются значения всех n-1 производных в начальной точке, если уравнение n-го порядка.
Функция odesolve позволяет решать двухточечные краевые задачи (дифференциальные уравнения с заданными значениями в нижней и верхней границах отрезка). Тогда начальные условия …
Система должна быть записана в форме Коши:
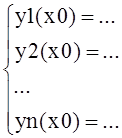 – начальные
условия (значения искомых функций в точке x0);
– начальные
условия (значения искомых функций в точке x0);
 – вектор первых производных искомых функций;
– вектор первых производных искомых функций;Функции mathcad для решения систем дифференциальных уравнений:
1) rkfixed (y, x0, xk, n, F) – возвращает матрицу значений функции.
y – вектор начальных условий;
x0 – нижняя граница интервала, на котором ищется решение;
xk – верхняя граница интервала, на котором ищется решение;
n – количество точек на интервале;
F – вектор первых производных искомых функций;
Используется метод Рунге-Кутта с фиксированным шагом.
2) Rkadapt (y, x0, xk, n, F) – возвращает матрицу значений функции.
Параметры такие же, как и в предыдущей функции. Отличие от предыдущей функции: в rkadapt шаг изменяется автоматически, поэтому эта функция работает медленнее, в rkfixed шаг фиксированный. Если функция изменяется медленно, то выгоднее пользоваться функцией rkadapt, так как это ведёт к уменьшению числа шагов. Используется адаптируемый метод Рунге-Кутта.
3) rkadapt (y, x0, xk, acc, F, k, S) – возвращает матрицу значений функции. Используется адаптируемый метод Рунге-Кутта. Количество шагов определяется точностью.
y – вектор начальных условий;
x0 – нижняя граница интервала, на котором ищется решение;
xk – верхняя граница интервала, на котором ищется решение;
acc – точность, чем меньше тем медленнее работает функция;
F – вектор первых производных искомых функций;
k – максимальное число точек на интервале;
S – минимальная разница между значениями функции в соседних точках;
4) bulstoer (y, x0, xk, acc, F, k, S) – возвращает матрицу значений решения системы обыкновенных дифференциальных уравнений. Параметры такие же, как и в предыдущей функции. Используется, если предполагается, что искомая функция и её производная гладкие и непрерывные на заданном интервале. Матрица значений решений рассчитывается по методу Булирша-Штера.
Примеры вызова данных функций для системы уравнений, данной выше:
rkadapt (y, 0, 5, 0.001, F, 0.0001)
bulstoer (y, 0, 5, 0.001, F, 0.0001)
5) Stiffb (y, x0, xk, n, F, J) – возвращает матрицу решений жёсткого дифференциального уравнения. Для расчёта используется метод Булиша-Штера
6) stiffb(y, x0, xk, acc, n, F, J) – возвращает матрицу решений в конечной точке жёсткого дифференциального уравнения. Для расчёта используется метод Булиша-Штера с переменным шагом;
7) Stiffr (y, x0, xk, n, F, J) – возвращает матрицу решений жёсткого дифференциального уравнения. Используется метод Розенброка;
8) stiffr(y, x0, xk, acc, F, J, k, S) – возвращает матрицу решений в конечной точке жёсткого дифференциального уравнения. Используется метод Розенброка с переменным шагом;
где все параметры, кроме J, те же, что и в предыдущих формулах.
J – матрица Якоби (якобиан), имеет следующий вид:
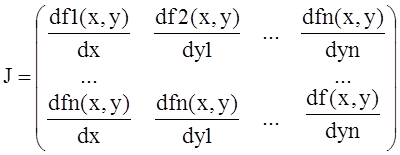
Размерность этой
матрицы n![]() (n+1).
(n+1).
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.