



Московский Авиационный Институт
Курсовая работа
по курсу дифференциальных уравнений на тему:
«Решение нелинейной краевой задачи методом конечных разностей»
Выполнил:
Проверил:
Оценка:
Москва 2003
Задание (№29).
Задача:
![]()
![]()
![]()
![]()
Решить данную краевую задачу методом конечных разностей. Расчет провести с шагами 0,1; 0,01 и 0,001. Для решения системы разностных уравнений использовать метод Ньютона. Представить полученные приближенные решения таблично и графически.
Метод конечных разностей.
Пусть
дано: ![]()
![]()
![]()
![]() (1)
(1)
При этом:
1)
функции a и g непрерывно дифференцируемы на ![]() и
и
![]() соответственно;
соответственно;
2)
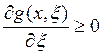
![]() при всех
при всех ![]() ,
,
![]() (*)
(*)
Введем
узлы ![]() , где
, где 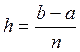 -
заданный шаг, а также
-
заданный шаг, а также 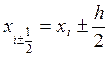
![]() . Положим
. Положим 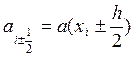 ,
, ![]() и
заменим правые производные центральными разностями
и
заменим правые производные центральными разностями 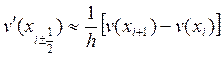 ,
,
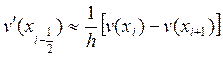 , а дифференциальное выражение
, а дифференциальное выражение ![]() - на разностное выражение вида:
- на разностное выражение вида:
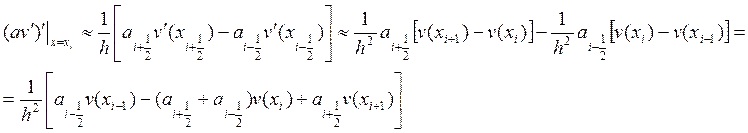
Воспользуемся последней разностной аппроксимацией для левой части ДУ (1), получим:
![]() ,
, ![]() (2)
(2)
Из
краевых условий (1) получаем краевые соотношения ![]()
![]() (3)
(3)
Система
уравнений (2), (3) является нелинейной системой из (n+1)-го
алгебраического (конечного) уравнения относительно (n+1)-й
неизвестных величин ![]() . Эта система имеет вид:
. Эта система имеет вид: ![]() , где
, где ![]() ,
(4)
,
(4)
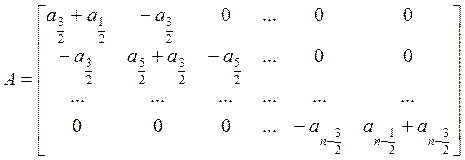
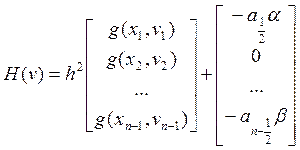 (5)
(5)
Система нелинейных уравнений (4) может быть решена методом Ньютона.
Метод Ньютона.
Пусть
![]() - матрица Якоби отображения
- матрица Якоби отображения ![]() . Тогда k-я
итерация метода Ньютона (k=1, 2, … ) состоит из двух
шагов:
. Тогда k-я
итерация метода Ньютона (k=1, 2, … ) состоит из двух
шагов:
1)
Решить относительно ![]() систему
линейных алгебраических уравнений
систему
линейных алгебраических уравнений
![]() , где
, где ![]() ,
, ![]() -известный
на k-ом шаге вектор.
-известный
на k-ом шаге вектор.
2)
Положить ![]()
В
качестве начального приближения можно брать вектор ![]() .
Из условий (*) следует, что рассматриваемая система нелинейных уравнений имеет единственное
решение. Из формулы (5) следует, что
.
Из условий (*) следует, что рассматриваемая система нелинейных уравнений имеет единственное
решение. Из формулы (5) следует, что 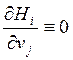 при
при ![]() , т.е матрица Якоби
, т.е матрица Якоби ![]() является диагональной.
Следовательно, матрица
является диагональной.
Следовательно, матрица ![]() - трехдиагональная.
- трехдиагональная.
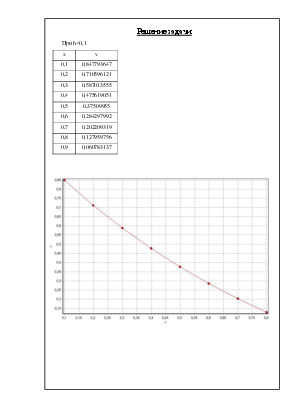
При h=0,1
|
x |
v |
|
0,1 |
0,847793647 |
|
0,2 |
0,710596121 |
|
0,3 |
0,587013555 |
|
0,4 |
0,475619051 |
|
0,5 |
0,37509955 |
|
0,6 |
0,284297992 |
|
0,7 |
0,202209319 |
|
0,8 |
0,127959756 |
|
0,9 |
0,060783137 |

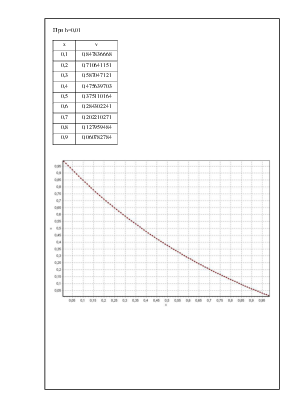
При h=0,01
|
x |
v |
|
0,1 |
0,847836668 |
|
0,2 |
0,710641151 |
|
0,3 |
0,587047121 |
|
0,4 |
0,475639703 |
|
0,5 |
0,375110164 |
|
0,6 |
0,284302241 |
|
0,7 |
0,202210271 |
|
0,8 |
0,127959484 |
|
0,9 |
0,060782784 |
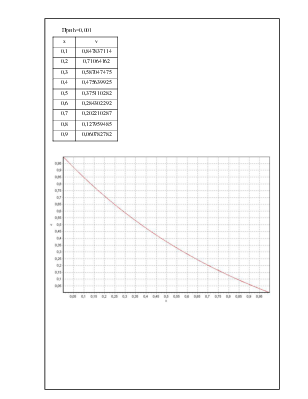
При h=0,001
|
x |
v |
|
0,1 |
0,847837114 |
|
0,2 |
0,71064162 |
|
0,3 |
0,587047475 |
|
0,4 |
0,475639925 |
|
0,5 |
0,375110282 |
|
0,6 |
0,284302292 |
|
0,7 |
0,202210287 |
|
0,8 |
0,127959485 |
|
0,9 |
0,060782782 |
При запуске программы все результаты подсчитываются автоматически. В появляющемся окне имеется 7 закладок:
· Результаты. В трех таблицах (для h=0,1, n=0,01 и n=0,001) выводится таблично приближенное решение краевой задачи.
· Матрица A для h=0,1.
· Матрица А для h=0,01.
· Матрица А для h=0,001.
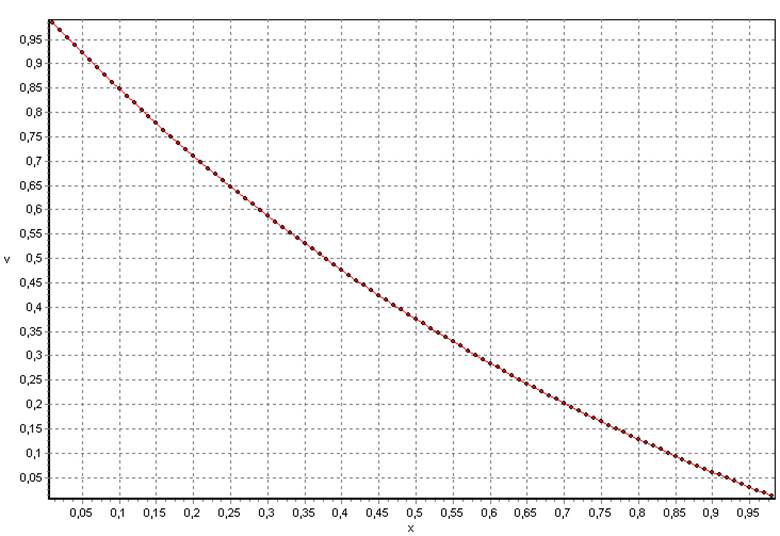
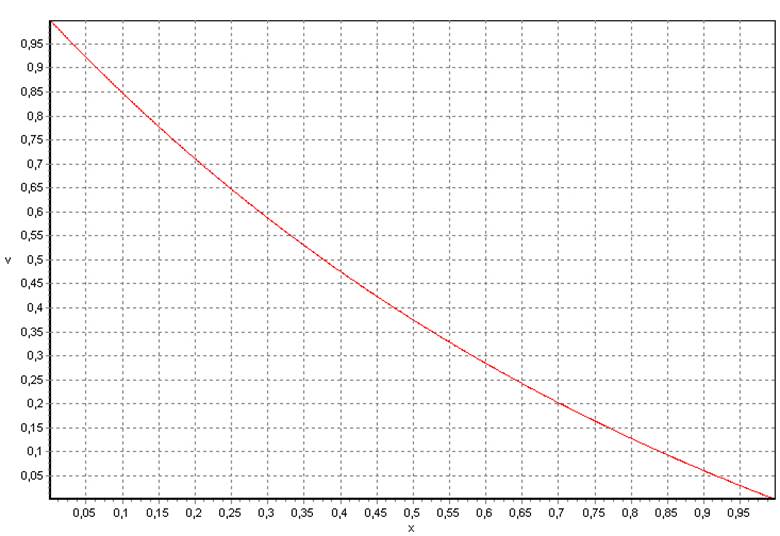
· График для h=0,1.
· График для h=0,01.
· График для h=0,001.
В ходе выполнения курсовой работы был изучен и применен метод конечных разностей для решения нелинейной краевой задачи, а также метод Ньютона при решении нелинейной системы уравнений. Для решения поставленной задачи вышеперечисленными методами была написана программа на языке C++ в среде программирования BuilderC++5.0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.