1. Виды нагрузок. Внутренние нагрузки. Метод сечения. Понятие о напряжении, деформациях и перемещениях. Гипотезы, применяемые в науке о сопротивлениях материалов
Надежность конструкции обеспечивается, если она сохраняет прочность, жесткость и устойчивость при гарантированной долговечности. Надежность и экономичность - противоречивые требования.
Классификация внешних сил.
Внешние силы, действующие на элемент конструкции, подразделяются на 3 группы: сосредоточенные силы, распределенные силы и объемные или массовые силы.
Внутренние силы. Метод сечений.
Внутри любого материала имеются внутренние межатомные силы. Если к твердому телу (рис.1,а) приложить внешние силы, то оно будет деформироваться. При этом изменяются расстояния между частицами тела, что в свою очередь приводит к изменению сил взаимного притяжения между ними. Отсюда возникают внутренние усилия. Для определения внутренних усилий используют метод сечения. Для этого тело мысленно рассекают плоскостью и рассматривают равновесие одной из его частей (рис. 1,б). Метод сечений позволяет выявить внутренние силовые факторы, но для оценки прочности необходимо знать внутренние силы в любой точке сечения. С этой целью введем числовую меру интенсивности внутренних сил – напряжение.
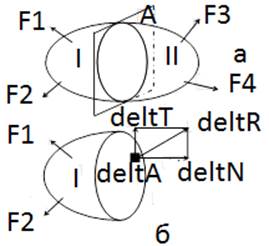
Понятие о
напряжениях. В сечение площадь ![]() . Равнодействующая внутренних
сил, действ. на площ.=
. Равнодействующая внутренних
сил, действ. на площ.= ![]() , модуль которой зависит от размера
площадки. Равнодействующую
, модуль которой зависит от размера
площадки. Равнодействующую ![]() разложим на 2 составл.:
разложим на 2 составл.: ![]() - по нормали к площадке и
- по нормали к площадке и ![]() - действующую по
площадке.
- действующую по
площадке.
 - среднее напряжением по площ.
- среднее напряжением по площ.
![]() . Вектор среднего
напряжения совп. по направлению с вект равнодействующей
. Вектор среднего
напряжения совп. по направлению с вект равнодействующей ![]() .
.
При уменьшении ![]() изменяются модуль и
направление равнодействующей
изменяются модуль и
направление равнодействующей ![]() , а вектор
, а вектор ![]() приближается к истинному значению
напряжения
приближается к истинному значению
напряжения ![]() в
заданной точке. Истинного напряжения выражается
в
заданной точке. Истинного напряжения выражается 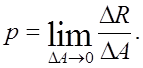
Отношение 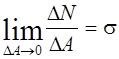 - нормальное
напряжение, а отношение
- нормальное
напряжение, а отношение 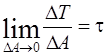 касательное напряжение.
касательное напряжение.
Зависимость между ![]() имеет вид
имеет вид ![]() .
.
Расчет реальных конструкций и их элементов является либо теоретически невозможным, либо практически неприемлемым по сложности. Поэтому в сопротивлении материалов применяется модель идеализированного деформируемого тела, включающая следующие допущения и упрощения:
1. Гипотеза сплошности и однородности: материал - однородная среда;св-ва матер-а во всех точках одинаковы,не завис от размеров тела.
2. Гипотеза об изотропности материала: физико-механ-ие св-ва матер = по всем напр-ям.
3. Гипотеза об идеальной упругости материала: тело восстанавливает первонач форму и разм после удаления причин, вызвавших его деформацию.
4. Гипотеза (допущение) о малости деформаций: деформации в точках тела счит.настолько малыми,что не оказ. существ-ого влияния на взаимное расположение нагрузок, приложенных к телу.
5. Допущение о справедливости закона Гука: перемещения точек конструкции в упругой стадии работы материала прямо пропорц силам, вызывающим эти перемещения.
6. Принцип независимости действия сил (принцип суперпозиции): результат воздействия неск.внешних факторов = ∑ результатов воздействия кажд из них,в отдельности, и не завис от последов-ти их приложения.
7. Гипотеза Бернулли о плоских сечениях: поперечные сечения, плоские и нормальные к оси стержня до прилож. к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.
8. Принцип Сен-Венана: в сечениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.
2. Статические моменты сечений. Центр тяжести плоского сечения.
При опр центра тяжести сечения нужно опред-ть значения стат-их моментов этого сечения.
|
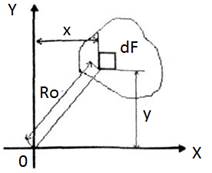
Стат-ми моментами площ сечения отн-но осей X и У называются опред-ые интегралы:
|
|
где F - площ сечения; X и у - координаты элемента площади dF. |
|
Если известно положение центра тяжести сечения то стат моменты сеч-я счит без интегралов: |
|
|
|
где Xc и Yc - координаты центра тяжести сечения. |
|
Из выражений можно определить координаты центра тяжести сечения Xc и Yc : |
|
|
|
Стат-ий момент сечения отн-но оси, проход-ей через центр тяж-ти=0. |
|
Оси, проход-ие че-з центр тяжести сечения –наз-ся центральными |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.