Исследование вынужденных колебаний динамической системы с полной степенью свободы

2.3.  Общая графическая схема  решения задачи и её описание

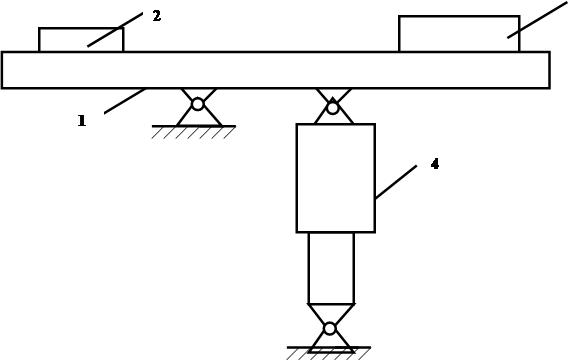
На рис. 1 показан общий вид испытательного стенда с качающейся балкой. Стенд служит для испытаний цилиндров гидропневматической подвески большегрузных автомобилей и определения проходных сечений клапанов амортизатора, обеспечивающих заданный режим колебаний.

Балка 1 может свободно качаться относительно оси 0 , если  придать ей начальный угол отклонения. На балке находятся грузы 2 и 3, которые могут перемещаться вдоль оси балки. Это позволяет изменять статическую нагрузку  на подвергающийся испытанию цилиндр 4 и изменять момент инерции балки 1 относительно оси 0.

В результате оптимизационных расчётов на математической модели большегрузного автомобиля удаётся установить числовые значения так называемых коэффициентов апериодичности,  входящих  в  характеристику амортизатора, для ходов сжатия Yс   и     отбоя  Y0.

Физическая реализация этих оптимальных параметров вызывает трудности по двум причинам: во-первых, подвеска имеет нелинейные характеристики, а коэффициент апериодичности однозначно характеризует свойства подвески с линейной характеристикой упругого элемента; во-вторых, конструктору необходимо знать, какой диаметр проходного отверстия амортизатора соответствует определённому значению коэффициента апериодичности. Однако такую зависимость в явном виде для цилиндра подвески с нелинейной характеристикой определить невозможно. Поэтому используется способ экспериментально-теоретический, заключающийся в следующем.

1.  С помощью математического моделирования получают эталонные графики переходных процессов для передней (задней) подвески автомобиля при определённых (оптимальных) значениях коэффициентов периодичности c0 , соответствующие определённой статической нагрузке на цилиндр и начальному отклонению системы от положения статического равновесия.

2.   Расчётным путём с помощью математической модели стенда определяются его необходимые настроечные параметры, затем стенд настраивается  и подготавливается к испытаниям.

3.  На стенде проводятся испытания цилиндра с определёнными проходными сечениями амортизатора для получения осциллограммы затухающих колебаний.

4.  Полученная осциллограмма сравнивается с эталонным графиком. Если кривые совпадают, значит, найдены оптимальные проходные сечения амортизатора, в противном случае нужно изменить проходные сечения амортизатора и вернуться к п.3.

			3

 

Рис. 1 Схема стендовой установки.

Так можно приближённо реализовать расчётные оптимальные параметры амортизатора, ощутимо сократив объём стендовых испытаний. Перейдём теперь к математическому описанию задачи.

Упругий элемент характеризуется выражением

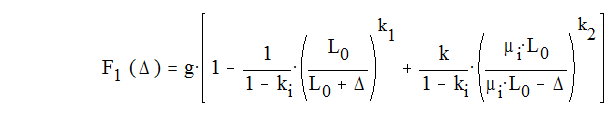
Для подвески с упругим гидропневматическим элементом без противодавления ki =0, и получаем новое выражение

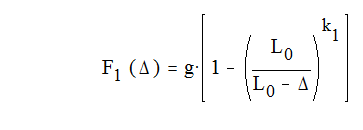
где индекс I определяет: при I=2 – заднюю подвеску автомобиля; g = 9,81; показатель политропы k = 1,25; L0  - идеализированная высота столба газа;  - деформация упругого элемента подвески.

Характеристика амортизатора задаётся формулой

                                                    .            .

.          2 w0i yc D   при D £ 0;                                                                             

F2i (D) =                      .            .                                                                                    

2 w0i y0 D   при D > 0,                                                                                 

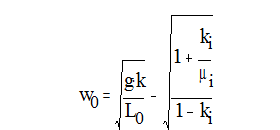С учётом ki=0  получаем: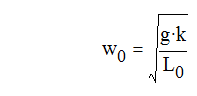  

где D = dD/dt .

Характеристика сухого трения задаётся выражением

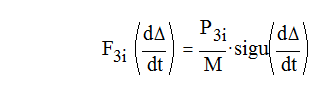
где P3i – сухое трение; М – подрессоренная масса.

А)                                                 Б)

 

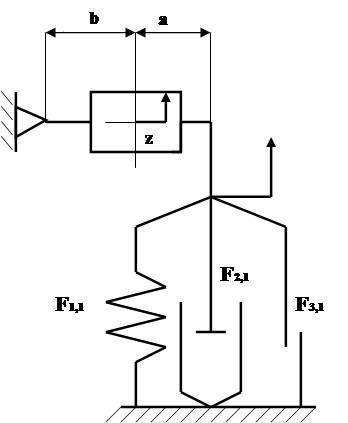
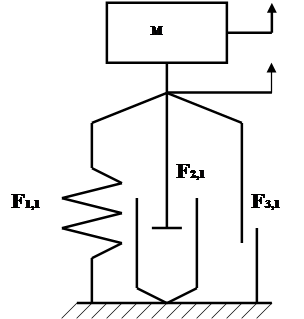
Рис. 2. Упрощённая расчётная схема:

А – передней подвески без учёта шины и неподрессоренных масс; Б – задней подвески

Колебания системы, кинематические схемы которой изображены на рис. 2, а, б, описываются нелинейным дифференциальным уравнением второго порядка:

..            .                   .                  . 

Z+Ai Fi (D) + A1 F2i (D) + Ai F3i (D) = 0   

.           .   

c начальными условиями при t = t0 Z(t0) = Z0 ; Z(t0) = Z0 = 0 , где D = Аi Z ;

 

1              при i = 1;

Ai =             

(a+b)/a    при i = 2;

Если перейти к переменной D, получим:  

..    ..

Z = D/Ai ;  Z = D/Ai ;  

0

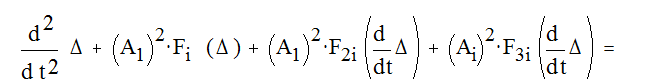
с начальными условиями при t = t0 :

.

D(t0) = D0 ;  D(t0) = 0.

Для того чтобы колебания подрессоренных  масс на стенде и автомобиля были одинаковыми, необходимо соблюдение для обоих случаев условий равенства начальных статистических нагрузок на цилиндр и кинетических энергий систем.

Рассмотрим переход от упрощённой схемы передней подвески к схеме стенда.

 

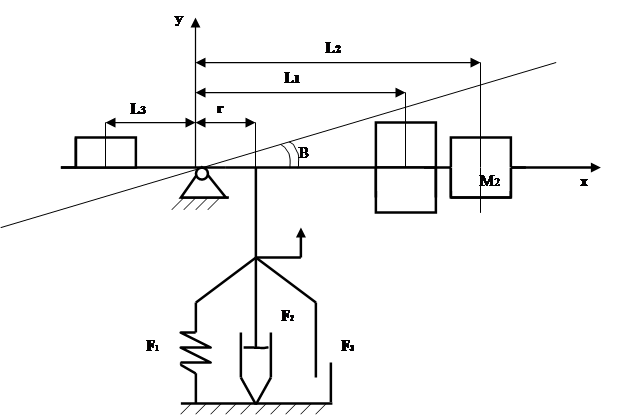Рис. 3. Расчётная схема стенда.

Условие равенства статических нагрузок

Кинетическая энергия балки с грузами

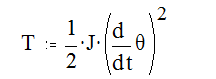
где J – момент инерции системы относительно оси вращения.

.      .

Если принять q = D/r  и   q =  D/r  , то

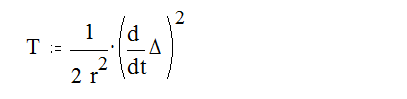
Кинетическая энергия передней подвески

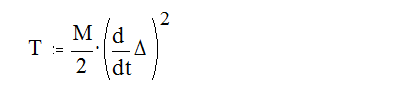
Поэтому условие равенства кинетических энергий

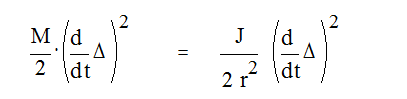
Получаем систему:

1.1

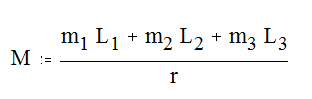
Для перехода от упрощённой схемы задней подвески к схеме стенда получаем:

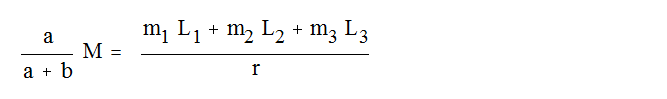
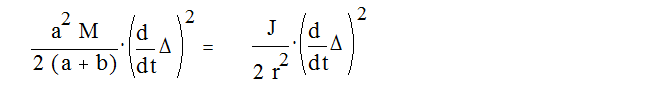
Таким образом получаем систему уравнений:

1.2

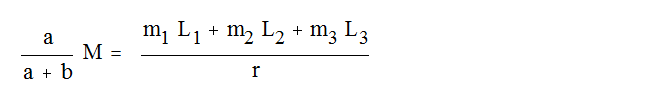
В общем случае выражение момента инерции зависит от переменных m₁, L₁, m₂, L₂, m_3, L₃. Приближённая формула имеет вид

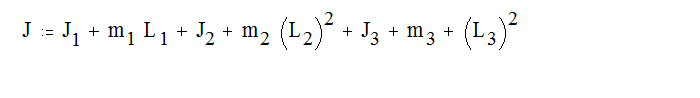
где J₁, J₂,  J₃ – моменты инерции масс относительно их центров инерции.

Подставив в систему 1.1 выражение J и определив два параметра, наиболее удобных для настройки стенда (например, m₂, L₃ ), разрешаем относительно их систему.

Решив систему 1.1 для передней подвески получим:

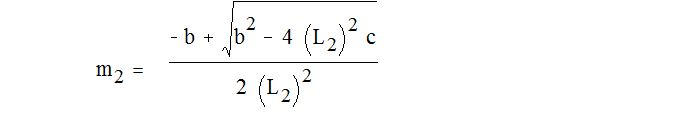
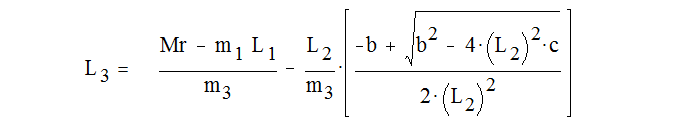
где

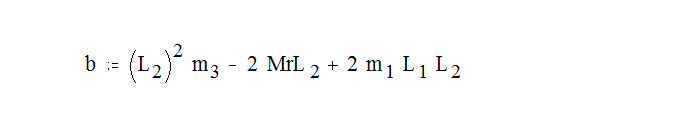
Для задней подвески получим аналогичные выражения для m₂ и L₂, если вместо r в формулах подставить выражение:

По описанной выше методике расчеты могут быть выполнены для любых значений исходных данных.