Составление математической модели движения тела под действием сил

2.   Алгоритмический анализ задачи.

2.1.Постановка задачи.

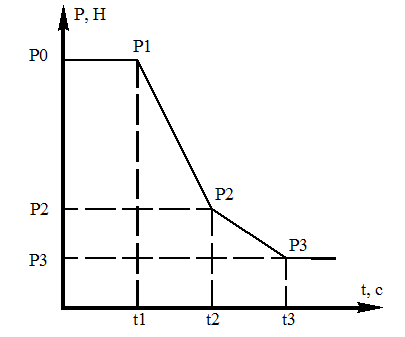Рис. 1 (а). Закон изменения силы P(t)

где t1=5с, t2=10с, t3=18с  – моменты времени изменения силы P(t). (t0=0).

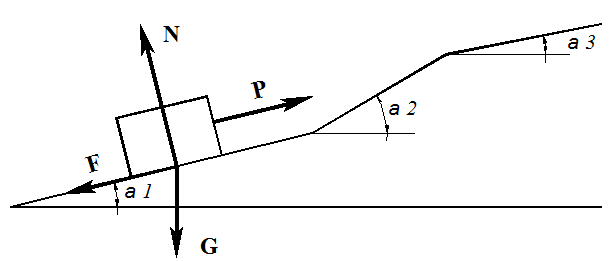
Рис. 1(б). Форма наклонной плоскости где x1=5м, x2=10м  – длина участка с углом наклона α1=25 град, α2=30 град, α3=35 град

Дано:

m =10 кг – масса груза; V₀ = 4.5 м/c; α = 25 град; t1 = 5 c; t2 = 10 c; t3 = 18 c;              

Pxo = 100 H; Px1 = 200 H; Px2 = 150 H; Px3 = 0H; f = 0,12;

Постановка задачи:

1.  Составить математическую модель движения тела под действием сил Px и Py.

2.   В пакете MathCAD по полученной математической модели определить значения функций перемещения, скорости, ускорения и траектории тела.

3.  Построить графики функций: перемещения в проекциях на оси x, y; вектора скорости и ускорения ; траектории полета тела.

4.  С помощью пакета MathConnex выполнить моделирование влияния Vo min на траекторию движения и определить при каком Vo min тело пролетит заданное расстояние.

5.  Для найденного Vo min построить графики траектории полета тела; вектора скорости и ускорения.

План решения:

a)  Необходимо провести аналитический расчет задачи, решив дифференциальные уравнения.

b)  Исследуем математическую модель в пакете Mathcad. Для чего:

¨  зададим начальные условия;

¨  определим зависимость сил Px и Py от времени;

Для заданных сил Px и Py запишем полученные аналитическим методом уравнения перемешения, скорости и ускорения.

c)  Произведем численный расчет данной маиематической модели с помощью встроенной функции rkfixed, которая позволяет найти решения дифференциальных уравнений.

d)  Сравниваем аналитический и численный методы.

e)  При помощи MathConnex находим угол, при котором будет полученно максимальное перемещение и анализируем полученные результаты.